我們對網格攻擊了解多少?
首先, 橢圓曲線數字簽名算法 (ECDSA) 是我們在許多代碼審查中看到的一種常見數字簽名方案。它具有一些理想的特性,但也可能非常脆弱,無法通過側信道攻擊來恢復私鑰,這種攻擊會洩露不到一位的秘密隨機數。
ECDSA是一種特殊形式的數字簽名算法(DSA)。DSA是一種相當常見的數字簽名方案,它由三種算法定義:密鑰生成、簽名和驗證。 密鑰生成算法生成私鑰和公鑰; 私鑰負責創建簽名; 公鑰負責驗證簽名。 簽名算法將消息和私鑰作為輸入並生成簽名。驗證算法以消息、簽名和公鑰為輸入,返回true或 的值false,表示簽名是否有效。
DSA 是為任何數學群定義的,只要離散對數問題對那個群來說是困難的,這個方案就是安全的。一個常用的組是整數模素數 p。
與這個組一起,我們將有一個組生成器 g 和一些加密安全的 哈希 函數 H。我們可以假設這 p , g 將 H 是常識。
密鑰生成首先從 x 模整數中 隨機選擇一個值p 。然後計算值 y = g^x mod p
簽名的私鑰為
x,公鑰為y。簽名密鑰必須保密,因為它允許進行簽名。
m 簽名算法根據消息和密鑰 x創建簽名 。首先,隨機生成一個群元素 k 。這被稱為隨機數,這在攻擊時很重要。
然後計算值 r = g^k mod p 並 s = ( k^-1 ( H ( m ) + xr )) mod p
這裡 k^- 1 , 是逆群, H ( m ) 是計算散列 m 並將結果解釋為整數模 p 的結果。
簽名定義為一對 ( r , s ). r (注意:如果or 值之一 s等於 0,則算法以 的新值重新開始 k )。
( r , s )驗證算法接收簽名、消息 和公鑰 y作為輸入 m 。讓 ŝ = s^-1 ,則算法返回 true 當且僅當 r , s ≠ 0 и r = ( g H ( m ) y r ) ŝ 。
此驗證檢查有效,因為 g^H( m ) y^r = g^H(m)+ xr = g^ks,因此 (g^H(m)y^r)^ŝ = g^k = r
如果無法偽造數字簽名方案,則認為它是安全的。
不變性具有正式的密碼學含義,但在較高層次上,它意味著您無法在不知道密鑰的情況下創建簽名(除非您已經復制了從密鑰創建的現有簽名)。DSA在離散日誌的假設下被證明是 不可能偽造的。
數字簽名是在數學組上定義的。當 DSA 與橢圓曲線群一起用作這個數學群時,我們稱它為 ECDSA。 橢圓曲線群 由橢圓曲線點組成,這些點是 的對 ,滿足 一些 的 ( x , y )方程 。對於這篇博文,你需要知道的是使用橢圓曲線你可以定義一個有限群,這意味著你得到群生成器,(橢圓曲線點),加法和點 乘操作 與你 完全 一樣可以用整數。因為它們形成一個有限群,生成器,y^2 = x^3 + ax + ba , bg g , 將有一個有限的順序, p。這篇博文不會解釋或要求您了解這些 橢圓曲線運算的工作原理。
密鑰 x 仍然是一個隨機值模整數 p 。ECDSA 工作方式與 相同 DSA,但使用不同的組。現在公鑰 y 仍然計算為 y = g^x ,只是 g 現在是橢圓曲線上的一個點。這意味著 y 也將是橢圓曲線上的一個點(以前 y 是整數模 p )。另一個區別是我們如何計算 r 的值。我們仍然像以前一樣生成隨機數 k 作為整數模 p。我們將計算 g^k ,但同樣,g 是橢圓曲線的一個點,因此 g^k 也是。因此,我們可以計算 ( x^k , y^k ) = g^k 並設置 r = x^k 。現在的意思 s 可以像以前一樣計算,我們得到我們的簽名 ( r , s ),它仍然是一個整數模 p ,和以前一樣。r 為了檢查,我們需要糾正我們計算的稍微不同的事實 。
因此,和以前一樣,我們 計算 的值
( g^H(m)y^r)^ŝ,但現在該值是橢圓曲線上的一個點,因此我們採用x該點的坐標並將其與我們的值進行比較r。
從重複使用的隨機數中 恢復 秘密密鑰NONCES
現在我們了解了它是什麼 ECDSA 以及它是如何工作的,讓我們來證明它的 脆弱性。同樣,由於這是一個數字簽名方案,因此絕不能將 密鑰 洩露給除簽名消息的人以外的任何人。
但是,如果簽名者曾經簽發過簽名並且還簽發過使用過的隨機數,那麼 攻擊者 可以立即恢復 密鑰。
假設我發布了 ( r , s ) 一條消息的 簽名m ,無意中發現我使用了 nonce k 。
由於 s = ( k^-1 ( H ( m ) + xr )), 我們可以很容易地計算出密鑰:
s = (k^-1(H(m) + xr))
ks = H(m) + xr
ks – H(m) = xr
x = r^-1(ks – H(m))
因此,簽名者不僅要保密他們的 私鑰,而且他們曾經生成的所有隨機數都是保密的。
即使簽名者對每個 nonce
NONCES保密,如果他不小心重複了一個 nonceNONCES(即使是針對不同的消息), 也可以 立即恢復秘密密鑰。
讓 ( r , s 1 ) 和 ( r , s 2 ) 成為在消息上創建的兩個簽名 m 1 並且 m 2 (分別)來自同一個隨機數—— k 因為它們具有相同的隨機數,所以 r 值將相同,所以這很容易被攻擊者檢測到:
s1 = k^-1(H(m1) + xr) and s2 = k^-1(H(m2) + xr)
s1 – s2 = k^-1(H(m1) – H(m2))
k(s1 – s2) = H(m1) – H(m2)
k = (s1 – s2)^-1(H(m1) – H(m2))
一旦我們使用上述公式恢復了隨機數 k ,我們就可以通過執行前面描述的攻擊來恢復私鑰。
讓我們消化一下。
如果 簽名的nonce
NONCES被洩露, 可以立即 恢復密鑰,這 會破壞我們的整個簽名方案。
此外,如果兩個 nonce 重複,無論消息是什麼, 攻擊者都 可以輕鬆檢測到這一點並立即 恢復密鑰,再次破壞我們的整個方案。
它非常脆弱,而且只有 輕攻擊!
但是有 一個新的 Lattice Attack 已經被詳細描述 (Joachim Breitner 和 Nadia Heninger)Йоахим Брайтнер и Надя Хенингер
文檔 [PDF]: 有偏差的 Nonce Sense:針對加密貨幣中弱 ECDSA 簽名的格攻擊
在比特幣區塊鏈中,我們發現了一筆交易:
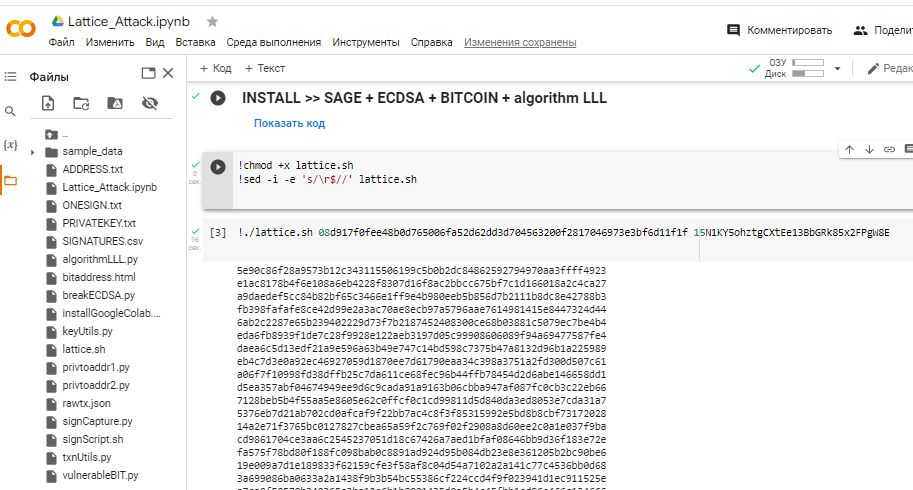
交易: 08d917f0fee48b0d765006fa52d62dd3d704563200f2817046973e3bf6d11f1f
比特幣地址: 15N1KY5ohztgCXtEe13BbGRk85x2FPgW8E
我們設法將假簽名相乘並應用網格
在GOOGLE COLAB 中安裝包 時使用 Python 腳本 algorithmLLL.py
安裝 >> SAGE + ECDSA + BITCOIN + 算法 LLL
我們 設法擺脫
Private Key了 .Bitcoin WalletECDSA
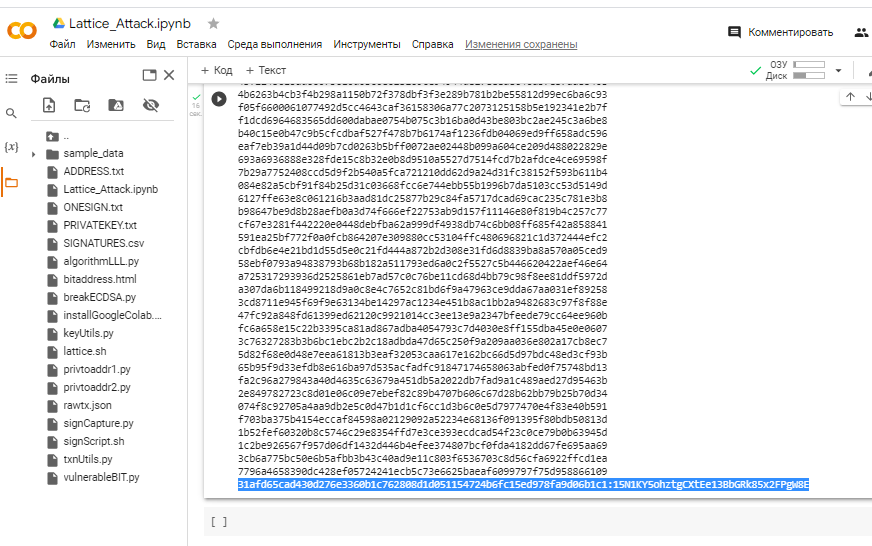



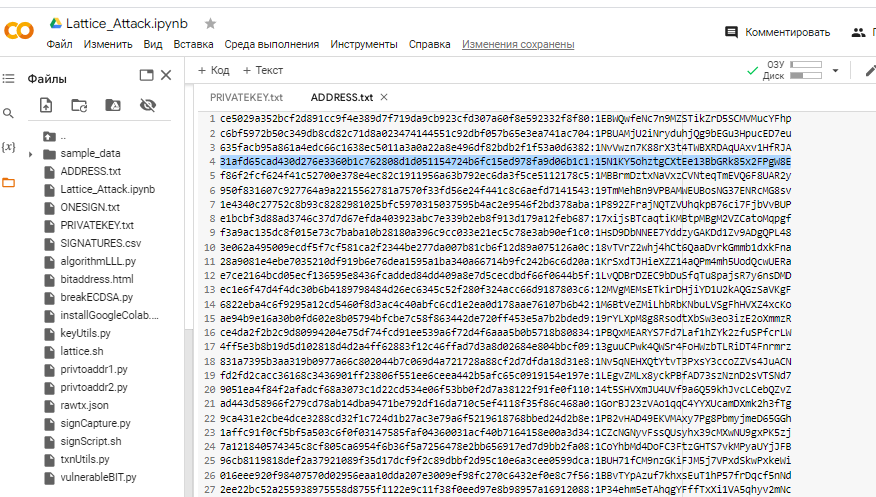
讓我們打開 bitaddress 並檢查:
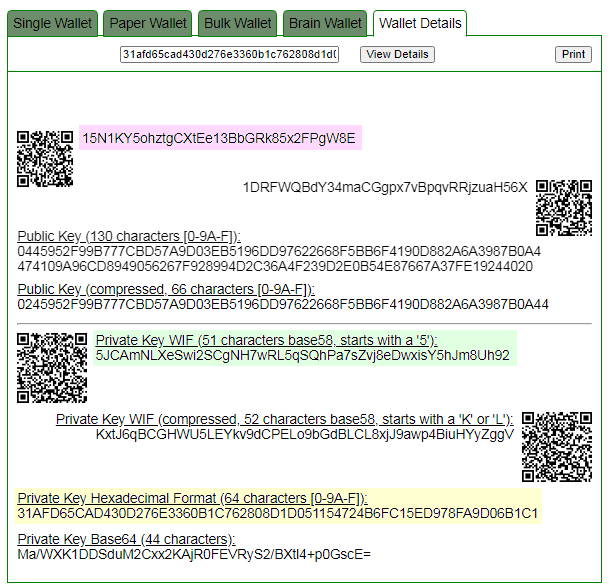
找到私鑰!
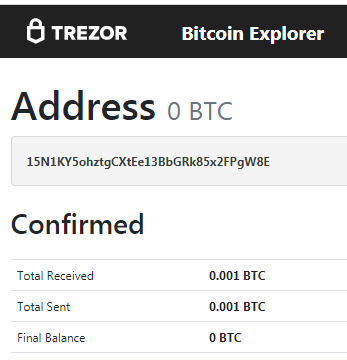
ADDR: 15N1KY5ohztgCXtEe13BbGRk85x2FPgW8E
WIF: 5JCAmNLXeSwi2SCgNH7wRL5qSQhPa7sZvj8eDwxisY5hJm8Uh92
HEX: 31AFD65CAD430D276E3360B1C762808D1D051154724B6FC15ED978FA9D06B1C1 該視頻是為CRYPTO DEEP TECH門戶網站創建的 ,以確保數據和 secp256k1 橢圓曲線密碼學的財務安全,以防止 BITCOIN 加密貨幣中的弱 ECDSA 簽名
https://youtu.be/YP4Xj6gUcf4 –視頻素材
cryptodeeptech@gmail.com – 所有問題的電子郵件
https://t.me/cryptodeep_tech – 通過 Telegram 提供技術支持
