secp256k1 橢圓曲線的有用且高效的算法

在本文中，我們將考慮幾種有用且有效的算法，用於 在 由短 Weierstrass 方程給出的 域 GF(p)上的橢圓曲線E

у^2 = х^3 + Ах + В 

•  生成曲線E上的點的算法 
•  加分算法
•  倍增點算法
•  尋找整數倍點的算法
•  尋找整數倍點的算法（標量乘法）
•   在具有給定大小 d 的 支持 supp  (D)的曲線E 上 構造除數 D的算法
•   Miller 算法用於從除數 D計算 Weil 函數f  _{n, P}的值  ，滿足 supp(D)  ∩ {P, O} = ∅
•  配對 威爾

有限域（或 Galois 域）上的模運算（整數）

1. x mod n 表示“除以 x 後的餘數 n”。換言之，如果 x = an + b 且 a, b ∈ 整數，且 0 ≤ b ≤ n − 1，則 x mod n = b  。
2. 反向 ：如果 ax = 1 mod n  ，則 a是x mod n 的倒數  。有兩種流行的解決方法  ： • 方法一 ：嘗試 a < n的每個值 ，只要 xa mod n = 1。  • 方法二 ：歐幾里德方法，通常用於解決大整數的逆問題，因此推薦使用使用方法1解決小整數反問題。

橢圓曲線點運算

 橢圓曲線 E上的點 P(x  ₀  ,y  ₀  ) 表示其 x  ₀ 和 y  ₀坐標 為域元素，  x  ₀ 和 y  ₀坐標 滿足方程。

1. 在橢圓曲線上加點 ：令 P、Q 和 R 為橢圓曲線上的三個點。添加點 P + Q = R。
2. 橢圓曲線上的雙點 ：令 P、Q 為橢圓曲線上的兩點。倍增點 P + P = 2P = Q
3. 點乘法 ：令 P 為曲線 E上的一個點 ，定義在等式中
   • 點乘 nP 定義為 nP = P + P + P + … + P  （  n 次），其中 n 為整數； nP 也是同一條 E曲線上的一個點 。
   • aP = O的最小自然數 a  稱為 P的階  。
   • 橢圓曲線密碼系統中廣泛需要點乘法。

分頻器

 曲線 E上的除數 (Divisor)  D 是表示 E上點的多重集的 便捷方式 ，寫為形式和

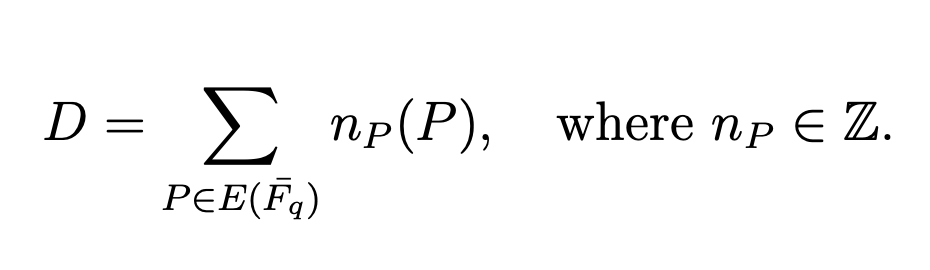
• E上所有除數的集合 用Div  _{F q}  (E) 表示  ，並形成一個群，其中除數的加法是自然的。
• 零因子：這是所有 n  _P  = 0 的因子，零因子 是 0 ∈ Div  _{F q}  (E)  。
• 如果域 F  _q 不具體，可以省略，簡單寫成 Div(E) 表示除數群。

函數 f 除以 E

函數 f 被 E的除數用於表示函數f 和 E 的交點（及其重數）   。

配對威爾

由e  m表示的 Weyl 配對  以一對點 P, Q ∈ E[m] 作為輸入 ，並 產生單位根 _m e  m (  P , Q) 作為輸出  。Weyl 對的雙線性由方程表示

e  _m  (P  ₁  + P  ₂  , Q) = e  _m  (P  ₁  , Q) * e  _m  (P2, В),

e  _m  (P, Q  ₁  + Q  ₂  ) = e  _m  (P, Q  ₁  ) * e  _m  (P, Q  ₂  )。

Weil 對 P 和 Q 是數

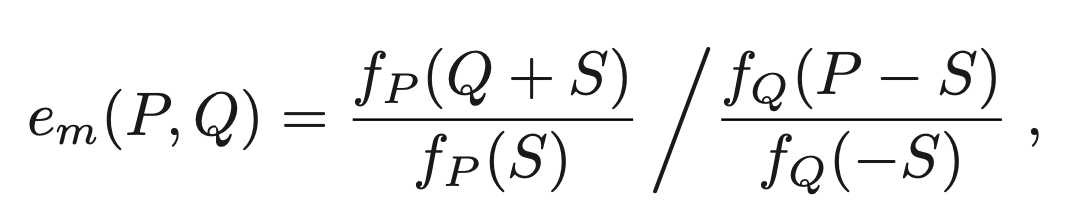
其中 S ∈ E 是滿足條件 S ∉ {O, P, −Q, P − Q} 的任意點 。（這確保右側的所有量都已定義且非零。）可以檢查 e  _m  (P,Q)的值不取決於f  _P  、  f  _Q 和 S 的選擇  。

一種高效的Weil配對計算算法

令 E 為橢圓曲線，令 P = (x  _P  ,y  _P  ) 和 Q = (x  _Q  , y  _{Q ) 為}E 上的非零點  。

令 λ為連接P 和 Q 的直線的斜率 ，或者如果P = Q 則E 在 P 處的  切線的斜率  。（如果直線是垂直的，我們設置 λ  = ∞。）定義函數 g  _{P, Q}  on  E 如下：

然後

div(g  _{P, Q}  ) = [P] + [Q] — [P + Q] —   [ O

米勒算法

令 m ≥並將m 的二進制擴展寫  為

m = m  ₀  + m  ₁  * 2 + m  ₂  * 2  ²  +···+ m  _{n — 1}  2  ^{n — 1}

因為 m  _i  ∈ {0, 1} 且 m  _{n — 1}  ≠ 0  。以下算法返回一個函數 f  _P 其除數滿足條件

div(  f  _P  ) =  m  [  P  ] — [  mP  ] — (  m — 1  ) [  O  ],

 其中算法使用的函數 g  _{T, T} 和 g  _{T, P在 (a) 中定義。}

特別地，如果 P ∈ E[m]  ，則 div(  f  _P  ) =  m  [  P  ] −  m  [  O  ]。

要求

• Python 3.5
• numpy

git clone https://github.com/demining/CryptoDeepTools.git

cd CryptoDeepTools/04AlgorithmsForSecp256k/

pip3 install numpy

├── Curves.py             <- Набор данных эллиптических кривых
├── Divisor.py            <- Создать делитель
├── EllipticCurve.py      <- Классы эллиптической кривой и точки на эллиптической кривой
├── EuclideanAlg.py       <- Расширенный алгоритм Евклида
├── Helper.py             <- Вспомогательные функции (обратные биты, мощность по модулю) 
├── Pairing.py            <- Спаривания Вейля, а так же Алгоритм Миллера
├── Tests.py              <- Модульные тесты для функций
├── Tonelli_ShanksAlg.py  <- Алгоритм Тонелли – Шенкса
├── main.py               <- main

來源

電報：  https: //t.me/cryptodeeptech

視頻素材：  https: //youtu.be/gFbiBCNPsFk

 密碼分析